- For educators
- English (US)
- English (India)
- English (UK)
- Greek Alphabet

This problem has been solved!
You'll get a detailed solution from a subject matter expert that helps you learn core concepts.

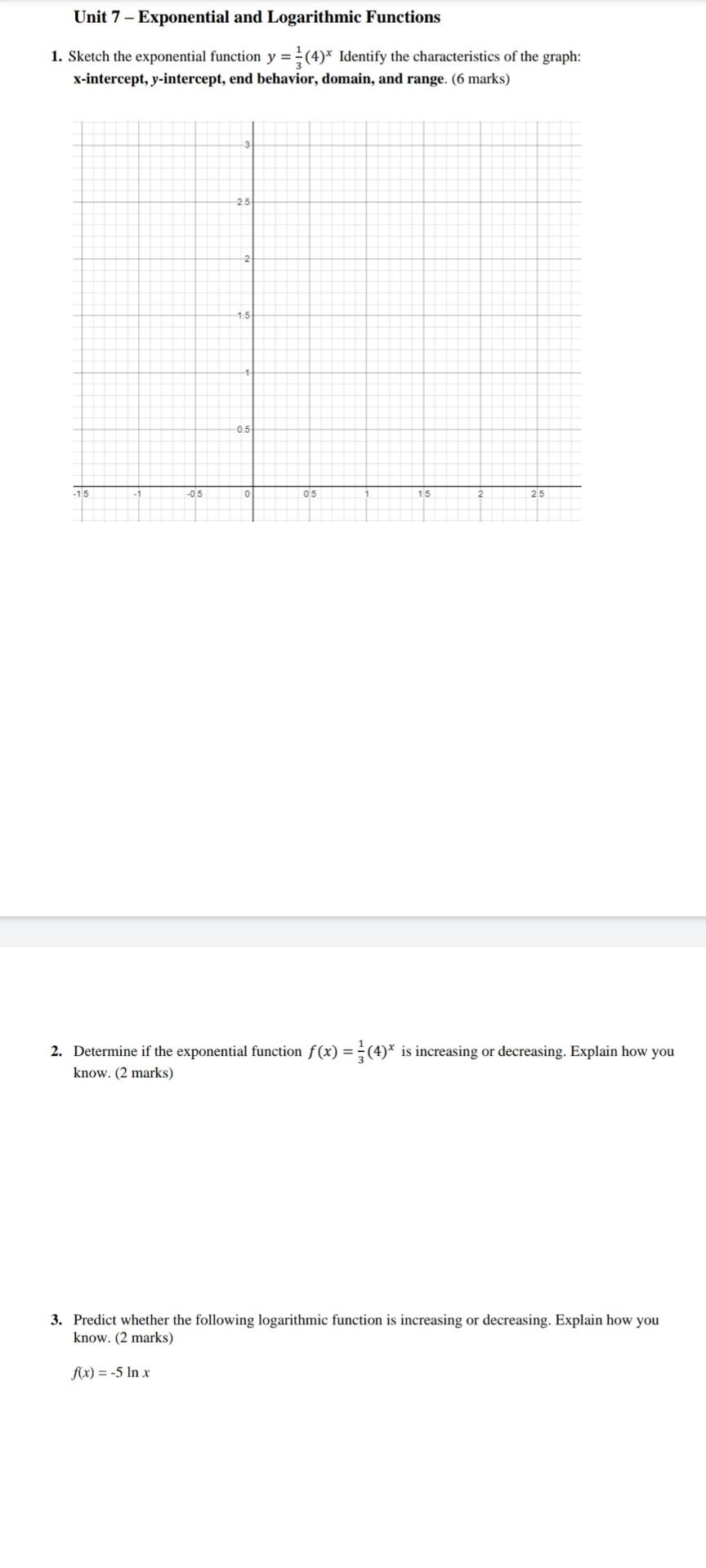
Question: Unit 7 - Exponential and Logarithmic Functions 1. Sketch the exponential function y = {(4)* Identify the characteristics of the graph: x-intercept, y-intercept, end behavior, domain, and range. (6 marks) 25 2 -0.5 -1.5 -0.5 0 05 15 25 2. ermine if the exponential know. (2 marks) f(x) = { (4)* is increasing or decreasing. Explain how you = 3. Predict whether
Assignment 2
This AI-generated tip is based on Chegg's full solution. Sign up to see more!
To find the -intercept of the exponential function , set to and solve for .

Not the question you’re looking for?
Post any question and get expert help quickly.

IMAGES
VIDEO
COMMENTS
Unit 6: Exponents & Exponential Functions Homework 7: Graphing Exponential Functions ** This is a 2-page document! ** Directions: Classify each function as an exponential growth or an exponential decay. Directions: Graph each function using a table of values, then identify its key characteristics. 5. 2 2 .25 Growth / Decay Domain: g 70 Range:
Gina Wilson (All Things Algebra}, 2015 '25 -. Name: Date: Unit 7: Exponential & Logarithmic Functions Homework 3: Intro to Logarithms Directions: Write each equation in exponential form. 1. log2128 = 7 2. 64 = 2 Directions: Write each equation in logarithmic form. 25b Directions: Evaluate each logarithm. Use the change of base formula when ...
Unit: Exponential Functions Date Homework Hour Graphing Exponential Functions Worksheet #2 Directions : Answer all questions. Show all work!!! Sketch the graph of each function. Then, state the Domain, Range, and Y-intercept, and change of Y-values of the function. 1. y =8•(12) x X Y -1 0 1
Trigonometry questions and answers. Name: Unit 7: Exponential & Logarithmic Functions Homework 1: Graphing Exponential Functions Date: Bell: ** This is a 2-page document! ** Directions: Classify each function as an exponential growth or an exponential decay. Sketch the curve 1. 10)-5 (x) 3. f) - 4 mo Directions: (a) Identify the parent function ...
Homework : Graphing Exponential Functions #1 - 3. Write the equation for the asymptote of each function below. Would the function's graph show exponential growth, or exponential decay? 1.
Answer 2: A. Slide 7 of 9 (answers read left to right then up and down) B. Slide 8 of 9 (answers read left to right then up and down) C. Slide 9 of 9 (answers read left to right then up and down) Sketch the graph of. Reflect the graph across the y-axis to show the function. Stretch the graph vertically by a factor of 3 to show the function.
7.1 - Exponential Functions Application 7.1 1. Solve for a: (1 216) −2 Ô+2 =36−1 2. The graph of U=2 ëis shown below. On the same graph, sketch U=2 ë+4+3. Label the horizontal asymptote! Sketch a graph of U=−2 ë−1+3. Label the horizontal asymptote. TRANSLATIONS For Review on how to translate, see Alg II 9.1 The graph of U=2 ë is ...
Exponential functions have definitions of the form f(x) = bx where b> 0 and b ≠ 1. The domain consists of all real numbers (− ∞, ∞) and the range consists of positive numbers (0, ∞). Also, all exponential functions of this form have a y -intercept of (0, 1) and are asymptotic to the x -axis.
UNIT 7Exponential Functions. 7.1 Exponential Growth. 7.2 Exponential Decay. 7.3 Linear vs. Exponential. Unit 7 Review.
Advanced Math. Advanced Math questions and answers. Unit 7 - Exponential and Logarithmic Functions 1. Sketch the exponential function y = { (4)* Identify the characteristics of the graph: x-intercept, y-intercept, end behavior, domain, and range. (6 marks) 25 2 -0.5 -1.5 -0.5 0 05 15 25 2. ermine if the exponential know. (2 marks) f (x) = { (4 ...