case study maths class 9 ch 12

• Statistics Class 9 Case Study Questions Maths Chapter 12

Last Updated on October 31, 2024 by XAM CONTENT

Hello students, we are providing case study questions for class 9 maths. Case study questions are the new question format that is introduced in CBSE board. The resources for case study questions are very less. So, to help students we have created chapterwise case study questions for class 9 maths. In this article, you will find case study questions for CBSE Class 9 Maths Chapter 12 Statistics. It is a part of Case Study Questions for CBSE Class 9 Maths Series.

Table of Contents

Case Study Questions on Statistics

Case Study Questions

Question 1:

India began its vaccination programmed on 16th January 2021. Within one year a massive population above 18 yr vaccinated upto 80% with double dose and 70% of children from age group 15 to 18 by taking 1st dose. This is all possible in short span of time due to combine efforts of governments and the citizens. The data collected by the government of vaccinated population is shown below.

On the basis of the above information, solve the following questions.

Q 1. Upper limit of the fourth class interval is: a. 30 b. 35 c. 35.5 d. 30.5

Q 2. The class mark of 3rd class interval is: a. 27 b. 27.5 c. 28 d. 28.5

Q 3. The number of people having ages more than 25 is (in million): a. 25 b. 26 c. 24 d. 23

Q 4. The number of peoples having maximum ages of 30 is (in million): a. 36 b. 34 c. 33 d. 38

Q 5. In a histogram, the class intervals on the groups are taken along: a. X-axis b. Y-axis c. Both a and b. d. in between X and Y axes

(1) (b) In given data, the fourth class-interval is 30-35.

The upper limit of fourth class-interval 30-35 is 35.

So, option (b) is correct.

(2) (b) In a given data, the third class is 25-30.

$\therefore$ The class mark of $25-30$ is $\frac{25+30}{2}$

$$ =\frac{55}{2}=27.5 $$

(3) (b) The number of peoples having ages more than 25 is 12+14 = 26 millions

(4) (a) The number of peoples having maximum ages of 30 is 14+10+12 = 36 millions

So, option (a) is correct.

(5) (a) In a histogram, the class intervals or the groups are taken along X-axis.

Understanding Statistics

Statistics: Science of collection, organisation, presentation, analysis and interpretation of numerical data.

Data: Facts or figures that are numeral or otherwise collected with a definite purpose.

Range of Data: The difference of the highest and lowest observation in the given data.

Frequency: The number of occurrence (or repeated) of an observation.

Class-size or Class-width: The difference between the upper and lower class limits.

Class Mark: The mid value of class-interval.

Frequency Distribution: The table in which the corresponding frequencies are written against each class.

Inclusive or Discontinuous Frequency Distribution: A frequency distribution in which the upper limit of one class differs from the lower limit of the succeeding class e.g., in class-interval 0-10, 11-20, we include both 0 and 10.

Exclusive or Continuous Frequency Distribution: A frequency distribution in which the upper limit of one class coincides with the lower limit of the succeeding class e.g., in class-interval 0-10, 10-20, we include 0 and exclude 10.

Graphical Representation of Data: Representing the data through graphs:

(i) Bar Graph: Pictorial representation of data in which rectangular bars of uniform width are drawn with equal spacing between them on one axis usually the X-axis. The value of the variable is shown on other axis i.e., Y-axis.

(ii) Histogram: Graphical representation of frequency distribution of continuous variables in the form of vertical rectangles, where class intervals represented as bases and frequencies represented as heights.

• Surface Areas and Volumes Class 9 Case Study Questions Maths Chapter 11
• Heron’s Formula Class 9 Case Study Questions Maths Chapter 10
• Circles Class 9 Case Study Questions Maths Chapter 9
• Quadrilaterals Class 9 Case Study Questions Maths Chapter 8
• Triangles Class 9 Case Study Questions Maths Chapter 7
• Lines and Angles Class 9 Case Study Questions Maths Chapter 6
• Introduction to Euclid’s Geometry Class 9 Case Study Questions Maths Chapter 5
• Linear Equations in Two Variables Class 9 Case Study Questions Maths Chapter 4
• Coordinate Geometry Class 9 Case Study Questions Maths Chapter 3

Polynomials Class 9 Case Study Questions Maths Chapter 2

Number systems class 9 case study questions maths chapter 1, topics from which case study questions may be asked.

• Histograms (with varying base lengths), and
• Frequency polygons.

Statistics is the science of collection, organisation, presentation, analysis and interpretation of numerical data.

Case study questions from the above given topic may be asked.

Helpful Links for CBSE Class 9 Preparation

• Download Chapter Tests for CBSE Class 9 Science
• Download Important MCQ Questions for CBSE Class 9 Physics
• Download Worksheets for CBSE Class 9 Science
• Download Case Study Questions for CBSE Class 9 Maths
• Download Sample Papers for CBSE Class 9
• Download HOTS with Solutions for CBSE Class 9 Science

Download Customised White Label Study Materials in MS Word Format

We are providing teaching resources to teachers and coaching institute looking for customised study materials in MS word format. Our High-quality editable study material which is prepared by the expert faculties are Highly useful for Teachers, Mentors, Tutors, Faculties, Coaching Institutes, Coaching Experts, Tuition Centers.

Frequently Asked Questions (FAQs) on Statistics Case Study

Q1: what is statistics in maths.

A1: Statistics is a branch of mathematics dealing with data collection, analysis, interpretation, and presentation. In CBSE Class 9, students learn how to organize and analyze data using tables, graphs, and other techniques to draw meaningful conclusions.

Q2: What are the types of data in statistics?

A2: Data in statistics is generally classified as: Primary Data: Data collected directly from an experiment, survey, or observation. Secondary Data: Data obtained from published sources or previously collected data.

Q3: What is the difference between a bar graph and a histogram?

A3: Bar Graph: Used to represent categorical data with rectangular bars. Each bar’s length represents the frequency of a category, and bars are usually separated by spaces. Histogram: Used to represent continuous data with adjacent bars, showing the frequency of intervals (or classes) of a continuous variable. In a histogram, bars touch each other.

Q4: How do you calculate the mean of a data set?

A4: The mean of a data set is calculated by adding all the observations together and dividing by the total number of observations.

Q5: What is a frequency distribution table, and why is it useful?

A5: A frequency distribution table organizes raw data into different classes or intervals to show the frequency (number of occurrences) of each interval. It helps in understanding data patterns and simplifying complex data for easier interpretation.

Q6: What is cumulative frequency, and how is it different from frequency?

A6: Frequency refers to the number of times a specific value or class appears in a data set. Cumulative Frequency is the sum of frequencies accumulated up to a particular class or value. It helps in determining how many data points fall below a certain class interval.

Q7: What is the purpose of the median in statistics?

A7: The median is the middle value in a data set when arranged in ascending or descending order. It is useful in understanding the central tendency of data, especially when there are outliers that might skew the mean.

Q8: What is the purpose of the median in statistics?

A8: Common mistakes include: Using incorrect formulas for specific shapes. Forgetting to square or cube units correctly. Mixing up radius and diameter (especially with spheres and cylinders). Not including all surfaces in total surface area calculations, such as forgetting the circular bases in cylinders.

Q9: Are there any online resources or tools available for practicing statistics case study questions?

A9: We provide case study questions for CBSE Class 9 Maths on our website. Students can visit the website and practice sufficient case study questions and prepare for their exams. If you need more case study questions, then you can visit Physics Gurukul website. they are having a large collection of case study questions for all classes.

Related Posts

cbseexpert.com

myCBSEguide

• Mathematics
• CBSE Class 9 Mathematics...

CBSE Class 9 Mathematics Case Study Questions

Table of Contents

myCBSEguide App

Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.

If you’re looking for a comprehensive and reliable study resource and case study questions for class 9 CBSE, myCBSEguide is the perfect door to enter. With over 10,000 study notes, solved sample papers and practice questions, it’s got everything you need to ace your exams. Plus, it’s updated regularly to keep you aligned with the latest CBSE syllabus . So why wait? Start your journey to success with myCBSEguide today!

Significance of Mathematics in Class 9

Mathematics is an important subject for students of all ages. It helps students to develop problem-solving and critical-thinking skills, and to think logically and creatively. In addition, mathematics is essential for understanding and using many other subjects, such as science, engineering, and finance.

CBSE Class 9 is an important year for students, as it is the foundation year for the Class 10 board exams. In Class 9, students learn many important concepts in mathematics that will help them to succeed in their board exams and in their future studies. Therefore, it is essential for students to understand and master the concepts taught in Class 9 Mathematics .

Case studies in Class 9 Mathematics

A case study in mathematics is a detailed analysis of a particular mathematical problem or situation. Case studies are often used to examine the relationship between theory and practice, and to explore the connections between different areas of mathematics. Often, a case study will focus on a single problem or situation and will use a variety of methods to examine it. These methods may include algebraic, geometric, and/or statistical analysis.

Example of Case study questions in Class 9 Mathematics

The Central Board of Secondary Education (CBSE) has included case study questions in the Class 9 Mathematics paper. This means that Class 9 Mathematics students will have to solve questions based on real-life scenarios. This is a departure from the usual theoretical questions that are asked in Class 9 Mathematics exams.

The following are some examples of case study questions from Class 9 Mathematics:

Class 9 Mathematics Case study question 1

There is a square park ABCD in the middle of Saket colony in Delhi. Four children Deepak, Ashok, Arjun and Deepa went to play with their balls. The colour of the ball of Ashok, Deepak,  Arjun and Deepa are red, blue, yellow and green respectively. All four children roll their ball from centre point O in the direction of   XOY, X’OY, X’OY’ and XOY’ . Their balls stopped as shown in the above image.

Answer the following questions:

Answer Key:

Class 9 Mathematics Case study question 2

• Now he told Raju to draw another line CD as in the figure
• The teacher told Ajay to mark  ∠ AOD  as 2z
• Suraj was told to mark  ∠ AOC as 4y
• Clive Made and angle  ∠ COE = 60°
• Peter marked  ∠ BOE and  ∠ BOD as y and x respectively

Now answer the following questions:

• 2y + z = 90°
• 2y + z = 180°
• 4y + 2z = 120°
• (a) 2y + z = 90°

Class 9 Mathematics Case study question 3

• (a) 31.6 m²
• (c) 513.3 m³
• (b) 422.4 m²

Class 9 Mathematics Case study question 4

How to Answer Class 9 Mathematics Case study questions

To crack case study questions, Class 9 Mathematics students need to apply their mathematical knowledge to real-life situations. They should first read the question carefully and identify the key information. They should then identify the relevant mathematical concepts that can be applied to solve the question. Once they have done this, they can start solving the Class 9 Mathematics case study question.

Students need to be careful while solving the Class 9 Mathematics case study questions. They should not make any assumptions and should always check their answers. If they are stuck on a question, they should take a break and come back to it later. With some practice, the Class 9 Mathematics students will be able to crack case study questions with ease.

Class 9 Mathematics Curriculum at Glance

At the secondary level, the curriculum focuses on improving students’ ability to use Mathematics to solve real-world problems and to study the subject as a separate discipline. Students are expected to learn how to solve issues using algebraic approaches and how to apply their understanding of simple trigonometry to height and distance problems. Experimenting with numbers and geometric forms, making hypotheses, and validating them with more observations are all part of Math learning at this level.

The suggested curriculum covers number systems, algebra, geometry, trigonometry, mensuration, statistics, graphing, and coordinate geometry, among other topics. Math should be taught through activities that include the use of concrete materials, models, patterns, charts, photographs, posters, and other visual aids.

CBSE Class 9 Mathematics (Code No. 041)

Class 9 Mathematics question paper design

The CBSE Class 9 mathematics question paper design is intended to measure students’ grasp of the subject’s fundamental ideas. The paper will put their problem-solving and analytical skills to the test. Class 9 mathematics students are advised to go through the question paper pattern thoroughly before they start preparing for their examinations. This will help them understand the paper better and enable them to score maximum marks. Refer to the given Class 9 Mathematics question paper design.

QUESTION PAPER DESIGN (CLASS 9 MATHEMATICS)

Mycbseguide: blessing in disguise.

Class 9 is an important milestone in a student’s life. It is the last year of high school and the last chance to score well in the CBSE board exams. myCBSEguide is the perfect platform for students to get started on their preparations for Class 9 Mathematics. myCBSEguide provides comprehensive study material for all subjects, including practice questions, sample papers, case study questions and mock tests. It also offers tips and tricks on how to score well in exams. myCBSEguide is the perfect door to enter for class 9 CBSE preparations.

Test Generator

Create question paper PDF and online tests with your own name & logo in minutes.

Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes

Related Posts

• Competency Based Learning in CBSE Schools
• Class 11 Physical Education Case Study Questions
• Class 11 Sociology Case Study Questions
• Class 12 Applied Mathematics Case Study Questions
• Class 11 Applied Mathematics Case Study Questions
• Class 11 Mathematics Case Study Questions
• Class 11 Biology Case Study Questions
• Class 12 Physical Education Case Study Questions

18 thoughts on “CBSE Class 9 Mathematics Case Study Questions”

This method is not easy for me

aarti and rashika are two classmates. due to exams approaching in some days both decided to study together. during revision hour both find difficulties and they solved each other’s problems. aarti explains simplification of 2+ ?2 by rationalising the denominator and rashika explains 4+ ?2 simplification of (v10-?5)(v10+ ?5) by using the identity (a – b)(a+b). based on above information, answer the following questions: 1) what is the rationalising factor of the denominator of 2+ ?2 a) 2-?2 b) 2?2 c) 2+ ?2 by rationalising the denominator of aarti got the answer d) a) 4+3?2 b) 3+?2 c) 3-?2 4+ ?2 2+ ?2 d) 2-?3 the identity applied to solve (?10-?5) (v10+ ?5) is a) (a+b)(a – b) = (a – b)² c) (a – b)(a+b) = a² – b² d) (a-b)(a+b)=2(a² + b²) ii) b) (a+b)(a – b) = (a + b

MATHS PAAGAL HAI

All questions was easy but search ? hard questions. These questions was not comparable with cbse. It was totally wastage of time.

Where is search ? bar

maths is love

Can I have more questions without downloading the app.

I love math

Hello l am Devanshu chahal and l am an entorpinior. I am started my card bord business and remanded all the existing things this all possible by math now my business is 120 crore and my business profit is 25 crore in a month. l find the worker team because my business is going well Thanks

I am Riddhi Shrivastava… These questions was very good.. That’s it.. ..

For challenging Mathematics Case Study Questions, seeking a writing elite service can significantly aid your research. These services provide expert guidance, ensuring your case study is well-researched, accurately analyzed, and professionally written. With their assistance, you can tackle complex mathematical problems with confidence, leading to high-quality academic work that meets rigorous standards.

It’s too hard

It’s very simple and easy question

Leave a Comment

Save my name, email, and website in this browser for the next time I comment.

CBSE Case Study Questions for Class 9 Maths - Pdf PDF Download

Cbse case study questions for class  9 maths.

CBSE Case Study Questions for Class 9 Maths are a type of assessment where students are given a real-world scenario or situation and they need to apply mathematical concepts to solve the problem. These types of questions help students to develop their problem-solving skills and apply their knowledge of mathematics to real-life situations.

Chapter Wise Case Based Questions for Class 9 Maths

The CBSE Class 9 Case Based Questions can be accessed from Chapetrwise Links provided below:

Chapter-wise case-based questions for Class 9 Maths are a set of questions based on specific chapters or topics covered in the maths textbook. These questions are designed to help students apply their understanding of mathematical concepts to real-world situations and events.

Chapter 1: Number System

• Case Based Questions: Number System

Chapter 2: Polynomial

• Case Based Questions: Polynomial

Chapter 3: Coordinate Geometry

• Case Based Questions: Coordinate Geometry

Chapter 4: Linear Equations

• Case Based Questions: Linear Equations - 1
• Case Based Questions: Linear Equations -2

Chapter 5: Introduction to Euclid’s Geometry

• Case Based Questions: Lines and Angles

Chapter 7: Triangles

• Case Based Questions: Triangles

Chapter 8: Quadrilaterals

• Case Based Questions: Quadrilaterals - 1
• Case Based Questions: Quadrilaterals - 2

Chapter 9: Areas of Parallelograms

• Case Based Questions: Circles

Chapter 11: Constructions

• Case Based Questions: Constructions

Chapter 12: Heron’s Formula

• Case Based Questions: Heron’s Formula

Chapter 13: Surface Areas and Volumes

• Case Based Questions: Surface Areas and Volumes

Chapter 14: Statistics

• Case Based Questions: Statistics

Chapter 15: Probability

• Case Based Questions: Probability

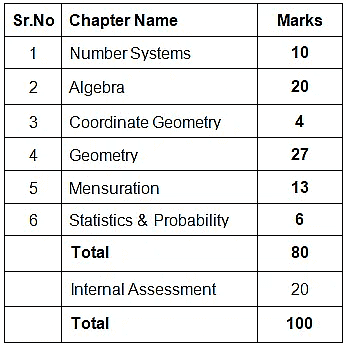
Weightage of Case Based Questions in Class 9 Maths

Why are Case Study Questions important in Maths Class  9?

• Enhance critical thinking:  Case study questions require students to analyze a real-life scenario and think critically to identify the problem and come up with possible solutions. This enhances their critical thinking and problem-solving skills.
• Apply theoretical concepts:  Case study questions allow students to apply theoretical concepts that they have learned in the classroom to real-life situations. This helps them to understand the practical application of the concepts and reinforces their learning.
• Develop decision-making skills:  Case study questions challenge students to make decisions based on the information provided in the scenario. This helps them to develop their decision-making skills and learn how to make informed decisions.
• Improve communication skills:  Case study questions often require students to present their findings and recommendations in written or oral form. This helps them to improve their communication skills and learn how to present their ideas effectively.
• Enhance teamwork skills:  Case study questions can also be done in groups, which helps students to develop teamwork skills and learn how to work collaboratively to solve problems.

In summary, case study questions are important in Class 9 because they enhance critical thinking, apply theoretical concepts, develop decision-making skills, improve communication skills, and enhance teamwork skills. They provide a practical and engaging way for students to learn and apply their knowledge and skills to real-life situations.

Class 9 Maths Curriculum at Glance

The Class 9 Maths curriculum in India covers a wide range of topics and concepts. Here is a brief overview of the Maths curriculum at a glance:

• Number Systems:  Students learn about the real number system, irrational numbers, rational numbers, decimal representation of rational numbers, and their properties.
• Algebra:  The Algebra section includes topics such as polynomials, linear equations in two variables, quadratic equations, and their solutions.
• Coordinate Geometry:  Students learn about the coordinate plane, distance formula, section formula, and slope of a line.
• Geometry:  This section includes topics such as Euclid’s geometry, lines and angles, triangles, and circles.
• Trigonometry: Students learn about trigonometric ratios, trigonometric identities, and their applications.
• Mensuration: This section includes topics such as area, volume, surface area, and their applications.
• Statistics and Probability:  Students learn about measures of central tendency, graphical representation of data, and probability.

The Class 9 Maths curriculum is designed to provide a strong foundation in mathematics and prepare students for higher education in the field. The curriculum is structured to develop critical thinking, problem-solving, and analytical skills, and to promote the application of mathematical concepts in real-life situations. The curriculum is also designed to help students prepare for competitive exams and develop a strong mathematical base for future academic and professional pursuits.

Students can also access Case Based Questions of all subjects of CBSE Class 9

• Case Based Questions for Class 9 Science
• Case Based Questions for Class 9 Social Science
• Case Based Questions for Class 9 English
• Case Based Questions for Class 9 Hindi
• Case Based Questions for Class 9 Sanskrit

Frequently Asked Questions (FAQs) on Case Based Questions for Class 9 Maths

What is case-based questions.

Case-Based Questions (CBQs) are open-ended problem solving tasks that require students to draw upon their knowledge of Maths concepts and processes to solve a novel problem. CBQs are often used as formative or summative assessments, as they can provide insights into how students reason through and apply mathematical principles in real-world problems.

What are case-based questions in Maths?

Case-based questions in Maths are problem-solving tasks that require students to apply their mathematical knowledge and skills to real-world situations or scenarios.

What are some common types of case-based questions in class 9 Maths?

Common types of case-based questions in class 9 Maths include word problems, real-world scenarios, and mathematical modeling tasks.

Top Courses for Class 9

Faqs on cbse case study questions for class 9 maths - pdf, study material, sample paper, semester notes, previous year questions with solutions, viva questions, mock tests for examination, extra questions, objective type questions, past year papers, video lectures, cbse case study questions for class 9 maths - pdf, practice quizzes, shortcuts and tricks, important questions.

CBSE Case Study Questions for Class 9 Maths - Pdf Free PDF Download

Importance of cbse case study questions for class 9 maths - pdf, cbse case study questions for class 9 maths - pdf notes, cbse case study questions for class 9 maths - pdf class 9, study cbse case study questions for class 9 maths - pdf on the app, welcome back, create your account for free.

Forgot Password

Change country.

• Andhra Pradesh
• Chhattisgarh
• West Bengal
• Madhya Pradesh
• Maharashtra
• Jammu & Kashmir
• NCERT Books 2022-23
• NCERT Solutions
• NCERT Notes
• NCERT Exemplar Books
• NCERT Exemplar Solution
• States UT Book
• School Kits & Lab Manual
• NCERT Books 2021-22
• NCERT Books 2020-21
• NCERT Book 2019-2020
• NCERT Book 2015-2016
• RD Sharma Solution
• TS Grewal Solution
• TR Jain Solution
• Selina Solution
• Frank Solution
• Lakhmir Singh and Manjit Kaur Solution
• I.E.Irodov solutions
• ICSE - Goyal Brothers Park
• ICSE - Dorothy M. Noronhe
• Micheal Vaz Solution
• S.S. Krotov Solution
• Evergreen Science
• KC Sinha Solution
• ICSE - ISC Jayanti Sengupta, Oxford
• ICSE Focus on History
• ICSE GeoGraphy Voyage
• ICSE Hindi Solution
• ICSE Treasure Trove Solution
• Thomas & Finney Solution
• SL Loney Solution
• SB Mathur Solution
• P Bahadur Solution
• Narendra Awasthi Solution
• MS Chauhan Solution
• LA Sena Solution
• Integral Calculus Amit Agarwal Solution
• IA Maron Solution
• Hall & Knight Solution
• Errorless Solution
• Pradeep's KL Gogia Solution
• OP Tandon Solutions
• Sample Papers
• Previous Year Question Paper
• Important Question
• Value Based Questions
• CBSE Syllabus
• CBSE MCQs PDF
• Assertion & Reason
• New Revision Notes
• Revision Notes
• Question Bank
• Marks Wise Question
• Toppers Answer Sheets
• Exam Paper Aalysis
• Concept Map
• CBSE Text Book
• Additional Practice Questions
• Vocational Book
• CBSE - Concept
• KVS NCERT CBSE Worksheets
• Formula Class Wise
• Formula Chapter Wise
• Toppers Notes
• Most Repeated Question
• Diagram Based Question
• Study Planner
• JEE Previous Year Paper
• JEE Mock Test
• JEE Crash Course
• JEE Sample Papers
• JEE Toppers Notes
• JEE Formula
• JEE Important Question
• JEE Mind Map
• JEE Integer-Numerical Type Question
• JEE Study Planner
• Important Info
• SRM-JEEE Previous Year Paper
• SRM-JEEE Mock Test
• VITEEE Previous Year Paper
• VITEEE Mock Test
• BITSAT Previous Year Paper
• BITSAT Mock Test
• Manipal Previous Year Paper
• Manipal Engineering Mock Test
• AP EAMCET Previous Year Paper
• AP EAMCET Mock Test
• COMEDK Previous Year Paper
• COMEDK Mock Test
• GUJCET Previous Year Paper
• GUJCET Mock Test
• KCET Previous Year Paper
• KCET Mock Test
• KEAM Previous Year Paper
• KEAM Mock Test
• MHT CET Previous Year Paper
• MHT CET Mock Test
• TS EAMCET Previous Year Paper
• TS EAMCET Mock Test
• WBJEE Previous Year Paper
• WBJEE Mock Test
• AMU Previous Year Paper
• AMU Mock Test
• CUSAT Previous Year Paper
• CUSAT Mock Test
• AEEE Previous Year Paper
• AEEE Mock Test
• UPSEE Previous Year Paper
• UPSEE Mock Test
• CGPET Previous Year Paper
• BCECE Previous Year Paper
• JCECE Previous Year Paper
• Crash Course
• Previous Year Paper
• NCERT Based Short Notes
• NCERT Based Tests
• NEET Sample Paper
• NEET Toppers Notes
• NEET Formula
• NEET Important Question
• NEET Assertion Reason Question
• NEET Study Planner
• Previous Year Papers
• Quantitative Aptitude
• Numerical Aptitude Data Interpretation
• General Knowledge
• Mathematics
• Agriculture
• Accountancy
• Business Studies
• Political science
• Enviromental Studies
• Mass Media Communication
• Teaching Aptitude
• Verbal Ability & Reading Comprehension
• Logical Reasoning & Data Interpretation
• CAT Mock Test
• CAT Important Question
• CAT Vocabulary
• CAT English Grammar
• MBA General Knowledge
• CAT Mind Map
• CAT Study Planner
• CMAT Mock Test
• SRCC GBO Mock Test
• SRCC GBO PYQs
• XAT Mock Test
• SNAP Mock Test
• IIFT Mock Test
• MAT Mock Test
• CUET PG Mock Test
• CUET PG PYQs
• MAH CET Mock Test
• MAH CET PYQs
• NAVODAYA VIDYALAYA
• SAINIK SCHOOL (AISSEE)
• Mechanical Engineering
• Electrical Engineering
• Electronics & Communication Engineering
• Civil Engineering
• Computer Science Engineering
• CBSE Board News
• Scholarship Olympiad
• School Admissions
• Entrance Exams
• All Board Updates
• Miscellaneous
• State Wise Books
• Engineering Exam

CBSE Class 9th Maths 2023 : 30 Most Important Case Study Questions with Answers; Download PDF

SHARING IS CARING If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.

CBSE Class 9 Maths exam 2022-23 will have a set of questions based on case studies in the form of MCQs. CBSE Class 9 Maths Question Bank on Case Studies given in this article can be very helpful in understanding the new format of questions.

Each question has five sub-questions, each followed by four options and one correct answer. Students can easily download these questions in PDF format and refer to them for exam preparation.

CBSE Class 9 All Students can also Download here Class 9 Other Study Materials in PDF Format.

• NCERT Solutions for Class 12 Maths
• NCERT Solutions for Class 10 Maths
• CBSE Syllabus 2023-24
• Social Media Channels
• Login Customize Your Notification Preferences
• CBSE Class 9th Exam 2024-25 : Skill Subject Sample Papers and Marking Scheme Released; Download PDF 3 September, 2024, 11:13 am
• CBSE Class 9th 2023-24 : Science Practical Syllabus; Download PDF 19 April, 2023, 4:52 pm
• CBSE Class 9 Maths Practice Book 2023 (Released By CBSE) 23 March, 2023, 6:16 pm
• CBSE Class 9 Science Practice Book 2023 (Released By CBSE) 23 March, 2023, 5:56 pm
• CBSE Class 9th Maths 2023 : 30 Most Important Case Study Questions with Answers; Download PDF 10 February, 2023, 6:20 pm
• CBSE Class 9th Maths 2023 : Important Assertion Reason Question with Solution Download Pdf 9 February, 2023, 12:16 pm
• CBSE Class 9th Exam 2023 : Social Science Most Important Short Notes; Download PDF 16 January, 2023, 4:29 pm
• CBSE Class 9th Mathematics 2023 : Most Important Short Notes with Solutions 27 December, 2022, 6:05 pm
• CBSE Class 9th English 2023 : Chapter-wise Competency-Based Test Items with Answer; Download PDF 21 December, 2022, 5:16 pm

CBSE Class 9th Exam 2024-25 : Skill Subject Sample Papers and Marking Scheme Released; Download PDF

CBSE has released the 2024-25 Class 9th skill subject sample papers and marking schemes. These resources help students understand the exam pattern, improve time management, and boost confidence. Download the PDFs from the CBSE official website to enhance your preparation. Practice consistently with these sample papers to excel in your exams and gain practical knowledge in key skill subjects.

• Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.

Case Study Questions for Class 9 Maths

• Post author: studyrate
• Post published:
• Post category: class 9th
• Post comments: 0 Comments

Are you preparing for your Class 9 Maths board exams and looking for an effective study resource? Well, you’re in luck! In this article, we will provide you with a collection of Case Study Questions for Class 9 Maths specifically designed to help you excel in your exams. These questions are carefully curated to cover various mathematical concepts and problem-solving techniques. So, let’s dive in and explore these valuable resources that will enhance your preparation and boost your confidence.

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

CBSE Class 9 Maths Board Exam will have a set of questions based on case studies in the form of MCQs. The CBSE Class 9 Mathematics Question Bank on Case Studies, provided in this article, can be very helpful to understand the new format of questions. Share this link with your friends.

If you want to want to prepare all the tough, tricky & difficult questions for your upcoming exams, this is where you should hang out.  CBSE Case Study Questions for Class 9  will provide you with detailed, latest, comprehensive & confidence-inspiring solutions to the maximum number of Case Study Questions covering all the topics from your  NCERT Text Books !

Table of Contents

CBSE Class 9th – MATHS: Chapterwise Case Study Question & Solution

Case study questions are a form of examination where students are presented with real-life scenarios that require the application of mathematical concepts to arrive at a solution. These questions are designed to assess students’ problem-solving abilities, critical thinking skills, and understanding of mathematical concepts in practical contexts.

Chapterwise Case Study Questions for Class 9 Maths

Case study questions play a crucial role in the field of mathematics education. They provide students with an opportunity to apply theoretical knowledge to real-world situations, thereby enhancing their comprehension of mathematical concepts. By engaging with case study questions, students develop the ability to analyze complex problems, make connections between different mathematical concepts, and formulate effective problem-solving strategies.

• Case Study Questions for Chapter 1 Number System
• Case Study Questions for Chapter 2 Polynomials
• Case Study Questions for Chapter 3 Coordinate Geometry
• Case Study Questions for Chapter 4 Linear Equations in Two Variables
• Case Study Questions for Chapter 5 Introduction to Euclid’s Geometry
• Case Study Questions for Chapter 6 Lines and Angles
• Case Study Questions for Chapter 7 Triangles
• Case Study Questions for Chapter 8 Quadilaterals
• Case Study Questions for Chapter 9 Areas of Parallelograms and Triangles
• Case Study Questions for Chapter 10 Circles
• Case Study Questions for Chapter 11 Constructions
• Case Study Questions for Chapter 12 Heron’s Formula
• Case Study Questions for Chapter 13 Surface Area and Volumes
• Case Study Questions for Chapter 14 Statistics
• Case Study Questions for Chapter 15 Probability

The above  Case studies for Class 9 Mathematics will help you to boost your scores as Case Study questions have been coming in your examinations. These CBSE Class 9 Maths Case Studies have been developed by experienced teachers of schools.studyrate.in for benefit of Class 10 students.

• Class 9 Science Case Study Questions
• Class 9 Social Science Case Study Questions

How to Approach Case Study Questions

When tackling case study questions, it is essential to adopt a systematic approach. Here are some steps to help you approach and solve these types of questions effectively:

• Read the case study carefully: Understand the given scenario and identify the key information.
• Identify the mathematical concepts involved: Determine the relevant mathematical concepts and formulas applicable to the problem.
• Formulate a plan: Devise a plan or strategy to solve the problem based on the given information and mathematical concepts.
• Solve the problem step by step: Apply the chosen approach and perform calculations or manipulations to arrive at the solution.
• Verify and interpret the results: Ensure the solution aligns with the initial problem and interpret the findings in the context of the case study.

Tips for Solving Case Study Questions

Here are some valuable tips to help you effectively solve case study questions:

• Read the question thoroughly and underline or highlight important information.
• Break down the problem into smaller, manageable parts.
• Visualize the problem using diagrams or charts if applicable.
• Use appropriate mathematical formulas and concepts to solve the problem.
• Show all the steps of your calculations to ensure clarity.
• Check your final answer and review the solution for accuracy and relevance to the case study.

Benefits of Practicing Case Study Questions

Practicing case study questions offers several benefits that can significantly contribute to your mathematical proficiency:

• Enhances critical thinking skills
• Improves problem-solving abilities
• Deepens understanding of mathematical concepts
• Develops analytical reasoning
• Prepares you for real-life applications of mathematics
• Boosts confidence in approaching complex mathematical problems

Case study questions offer a unique opportunity to apply mathematical knowledge in practical scenarios. By practicing these questions, you can enhance your problem-solving abilities, develop a deeper understanding of mathematical concepts, and boost your confidence for the Class 9 Maths board exams. Remember to approach each question systematically, apply the relevant concepts, and review your solutions for accuracy. Access the PDF resource provided to access a wealth of case study questions and further elevate your preparation.

Q1: Can case study questions help me score better in my Class 9 Maths exams?

Yes, practicing case study questions can significantly improve your problem-solving skills and boost your performance in exams. These questions offer a practical approach to understanding mathematical concepts and their real-life applications.

Q2: Are the case study questions in the PDF resource relevant to the Class 9 Maths syllabus?

Absolutely! The PDF resource contains case study questions that align with the Class 9 Maths syllabus. They cover various topics and concepts included in the curriculum, ensuring comprehensive preparation.

Q3: Are the solutions provided for the case study questions in the PDF resource?

Yes, the PDF resource includes solutions for each case study question. You can refer to these solutions to validate your answers and gain a better understanding of the problem-solving process.

You Might Also Like

Mcq questions of class 9 social science history chapter 7 history and sport the story of cricket with answers, mcq class 9 social science geography india size and location quiz with answers, class 9 science case study questions chapter 1 matter in our surroundings, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

My Study materials – Kumar

Ltsm (learning and teaching study materials), maths class ix case study questions.

MATHS CLASS IX CASE STUDY BASED QUESTIONS

FOR ANNUAL EXAM 2020-21

Maths Case Study Question 01

Click to access maths-ix-case-study-question-01.pdf

Maths Case Study Question 02

Click to access maths-ix-case-study-question-02.pdf

Maths Case Study Question 03

Click to access maths-ix-case-study-question-03.pdf

Maths Case Study Question 04

Click to access maths-ix-case-study-question-04.pdf

Maths Case Study Question 05

Click to access maths-ix-case-study-question-05.pdf

Maths Case Study Question 06

Click to access maths-ix-case-study-question-06.pdf

Maths Case Study Question 07

Click to access maths-ix-case-study-question-07.pdf

Maths Case Study Question 08

Click to access maths-ix-case-study-question-08.pdf

Maths Case Study Question 09

Click to access maths-ix-case-study-question-09.pdf

Maths Case Study Question 10

Click to access maths-ix-case-study-question-10.pdf

Maths Case Study Question 11

Click to access maths-ix-case-study-question-11.pdf

Maths Case Study Question 12

Click to access maths-ix-case-study-question-12.pdf

Maths Case Study Question 13

Click to access maths-ix-case-study-question-13.pdf

Maths Case Study Question 14

Click to access maths-ix-case-study-question-14.pdf

Maths Case Study Question 15

Click to access maths-ix-case-study-question-15.pdf

Maths Case Study Question 16

Click to access maths-ix-case-study-question-16.pdf

Maths Case Study Question 17

Click to access maths-ix-case-study-question-17.pdf

Maths Case Study Question 18

Click to access maths-ix-case-study-question-18.pdf

Maths Case Study Question 19

Click to access maths-ix-case-study-question-19.pdf

Maths Case Study Question 20

Click to access maths-ix-case-study-question-20.pdf

Maths Case Study Question 21

Click to access maths-ix-case-study-question-21.pdf

Maths Case Study Question 22

Click to access maths-ix-case-study-question-22.pdf

Maths Case Study Question 23

Click to access maths-ix-case-study-question-23.pdf

Maths Case Study Question 24

Click to access maths-ix-case-study-question-24.pdf

Maths Case Study Question 25

Click to access maths-ix-case-study-question-25.pdf

Maths Case Study Question 26

Click to access maths-ix-case-study-question-26.pdf

Maths Case Study Question 27

Click to access maths-ix-case-study-question-27.pdf

Maths Case Study Question 28

Click to access maths-ix-case-study-question-28.pdf

Maths Case Study Question 29

Click to access maths-ix-case-study-question-29.pdf

Maths Case Study Question 30

Click to access maths-ix-case-study-question-30.pdf

Share this:

• Copy shortlink
• Report this content
• Manage subscriptions

CBSE Class 9 Maths 30 Most Important Case Study Questions with Answers

Cbse class 9 maths 30 most important case study questions with answers download here free in pdf format..

CBSE Class 9 Maths exam 2023 will have a set of questions based on case studies in the form of MCQs. CBSE Class 9 Maths Question Bank on Case Studies given in this webpage can be very helpful in understanding the new format of questions.

Each question has five sub-questions, each followed by four options and one correct answer. Candidates can easily download these questions in PDF format and refer to them for exam preparation 2023.

Related Articles

Up board exam result 2023 : upmsp 10th, 12th results expected soon, खुशखबरी -यूपी के हाईस्कूल और इंटरमीडिएट की बोर्ड परीक्षा 2022 के टॉपर्स का 4.73 करोड़ रुपये से सम्मान करेगी यूपी सरकार, neet ug exam 2023 on may 7; here are some useful tips and pointers for preparation, cbse class 12 exam economics analysis, review & question paper with answer key 2023, leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

• CBSE Board: आ गई 10वीं-12वीं की डेटशीट, अब जान लें ये जरूरी नियम December 30, 2022

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Category: Case Study Questions for Class 9 Maths

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 9 Maths Chapter 12 Herons Formula

Case study questions for class 9 maths chapter 9 areas of parallelograms and triangles, case study questions for class 9 maths chapter 6 lines and angles, case study questions for class 9 maths chapter 7 triangles, case study questions for class 9 maths chapter 5 introduction to euclid’s geometry, case study and passage based questions for class 9 maths chapter 14 statistics, case study questions for class 9 maths chapter 1 real numbers, case study questions for class 9 maths chapter 4 linear equations in two variables, case study questions for class 9 maths chapter 3 coordinate geometry, case study questions for class 9 maths chapter 15 probability, case study questions for class 9 maths chapter 13 surface area and volume, case study questions for class 9 maths chapter 10 circles, case study questions for class 9 maths chapter 9 quadrilaterals, case study questions for class 9 maths chapter 2 polynomials.

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs

Class 9th Maths - Linear Equations in Two Variables Case Study Questions and Answers 2022 - 2023

QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 9th Maths Subject - Linear Equations in Two Variables, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.

QB365 - Question Bank Software

Linear equations in two variables case study questions with answer key.

9th Standard CBSE

Final Semester - June 2015

Mathematics

(ii) Find the length of the outer boundary of the layout.

(iii) The pair of linear equation in two variables formed from the statements are (a) x + y = 13, x + y = 9 (b) 2x + y = 13, x + y = 9 (c) x + y = 13, 2x + y = 9 (d) None of the above (iv) Which is the solution satisfying both the equations formed in (iii)?

(v) Find the area of each bedroom.

(iii) Find the cost of one pen?

(iv) Find the total cost if they will purchase the same type of 15 notebooks and 12 pens.

(v) Find whose estimation is correct in the given statement.

(b) How to represent the above situation in linear equations in two variables ?

(c) If Sita contributed Rs. 76, then how much was contributed by Gita ?

(d) If both contributed equally, then how much is contributed by each?

(e) Which is the standard form of linear equations x = – 5 ?

(ii) Which is the solution of the equations formed in (i)?

(c) If the cost of one notebook is Rs. 15 and cost of one pen is 10, then find the total amount.

(d) If the cost of one notebook is twice the cost of one pen, then find the cost of one pen?

(e) Which is the standard form of linear equations y = 4 ?

(b) If the number of children is 15, then find the number of adults?

(c)  If the number of adults is 12, then find the number of children?

(d) Find the value of b, if x = 5, y = 0 is a solution of the equation 3x + 5y = b.

(e) Which is the standard form of linear equations in two variables: y - x = 5?

(b) If the cost of chocolates A is 5, then find the cost of chocolates B?

(c) Which of the follwing point lies on the line x + y = 7?

(d) The point where the line x + y = 7 intersect y-axis is 

(e) For what value of k, x = 2 and y = -1 is a soluation of x + 3y -k = 0.

*****************************************

Related 9th standard cbse mathematics materials, other 9th standard cbse materials.

Class 10th Social Science - Pastoralists Case Study Questions and Answers 2022 - 2023

Class 9th social science - forest society and colonialism case study questions and answers 2022 - 2023, class 9th social science - nazism and the rise of hitler case study questions and answers 2022 - 2023, class 9th social science - socialism in europe and the russian revolution case study questions and answers 2022 - 2023, class 9th social science - the french revolution case study questions and answers 2022 - 2023.

Class 9th Science - Work and Energy Case Study Questions and Answers 2022 - 2023

Class 9th science - force and laws of motion case study questions and answers 2022 - 2023, class 9th science - motion case study questions and answers 2022 - 2023, class 9th science - the fundamental unit of life case study questions and answers 2022 - 2023, class 9th science - is matter around us pure case study questions and answers 2022 - 2023, class 9th science - matter in our surroundings case study questions and answers 2022 - 2023, xam idea 9th standard economics ncert solutions for food security in india, xam idea 9th standard economics ncert solutions for poverty as a challenge, xam idea 9th standard economics ncert solutions for people as resource, xam idea 9th standard economics ncert solutions for the story of village palampur, tamilnadu stateboard 9th standard cbse study materials.

Tamilnadu Stateboard 9th Standard CBSE Subjects

Talk to our experts

1800-120-456-456

Important Questions for CBSE Class 9 Maths Chapter 12 - Statistics

• Class 9 Important Question
• Chapter 14: Statistics

CBSE Class 9 Maths Chapter-14 Important Questions - Free PDF Download

Class 9 Maths Chapter 12 Important Questions from Statistics chapter includes the content developed by experts on various topics of collection and representation of data, graphical representation of data using a bar graph, Histogram, and Pie Chart, Measures of central tendency, i.e., mean, median, and mode and exercise problems.

Vedantu provides free PDF solutions on Important Questions for Class 9 Maths Chapter 12 Statistics according to NCERT Solutions curriculum which is useful for students to prepare for their exams. Also, Class 9 Maths Chapter 12 Extra Questions are included in this PDF which is useful for students to practise extra problems on Statistics chapter so that they can ace any exams. Students can download NCERT Solutions Maths Class 9 to help you to revise the complete Syllabus and score more marks in your examinations. Students can also avail of NCERT Solutions Class 9 Science from our website.

Download CBSE Class 9 Maths Important Questions 2024-25 PDF

Also, check CBSE Class 9 Maths Important Questions for other chapters:

Topics Covered in CBSE Class 9 Maths Chapter 12- Statistics

Below are the important topics of Class 9 Maths Chapter 12 Statistics:

Introduction

Collection of data 

Presentation of data

Measure of central tendency 

Important Questions for Class 9 Maths Chapter 12 – Statistics

1. If the mean of $2,4,6,8,{\text{x}},{\text{y}}$ is 5 then find the value of x+y.

2. Write the class mark of $90 - 110$ group.

3. If the ratio of mean and median of a certain data is 2: 3, then find the ratio of its mode and mean.

4. Tally marks are used to find ...............

Ans: Frequency

5. The following marks were obtained by the students in a test. 81,72,90,90,86,85,92,70,71,83,89,95,85,79,62. What is the range? 

6. In a histogram, each class rectangle is constructed with base as

1. frequency

2. class interval

4. size of the class

Ans: class interval

Section  B

7. The mean of 10 numbers is 20. If 5 is subtracted from every number, what will be the new mean?

Ans: Let ${{\text{x}}_1},{{\text{x}}_2}, \ldots {x_{10}}$ be 10 numbers with their mean equal to 20 .

$\bar X = \dfrac{1}{n}\left( {\sum{{x_i}} } \right)$

$20 = \dfrac{{{x_1} + {x_2} + \ldots .. + {x_{20}}}}{{10}}$

$\Rightarrow 200 = {{\text{x}}_1} + {x_2} +  \ldots . + {x_{10}}$

New numbers are ${{x}_{1}}-5,\ {{x}_{2}}-5,\ \ldots \text{}\!\!~\!\!\text{ }\ldots ,\ {{x}_{10}}-5$

Let $\bar X$ be the mean of new number.

$\bar{X}\text{ }\!\!~\!\!\text{}=\dfrac{\left( {{x}_{1}}-5 \right)+\left( {{x}_{2}}-5 \right)+\text{}\!\!~\!\!\text{ }\ldots .+\left( {{x}_{10}}-5 \right)}{10}$

$X=\dfrac{\left({{x}_{1}}+{{x}_{2}}+\text{ }\!\!~\!\!\text{ }\ldots \text{ }\!\!~\!\!\text{}\ldots \text{ }\!\!~\!\!\text{ }+{{x}_{10}} \right)-5\times 10}{10}$

$=\dfrac{200-50}{10}=15$

8. Find the mean of the first 10 even natural no.

Ans: \[\bar{x}\ =\ \dfrac{2+4+6+8+10+12+14+16+18+20}{10}\ =\ \dfrac{10\ \times \ 11}{10}\ =\ 11\]

9. Calculate the mean for the following distribution. 

$\begin{array}{*{20}{c}}{\mathbf{x}}&5&6&7&8&9 \\ {\mathbf{f}}&4&8&{14}&{11}&3 \\ \end{array}$

10. Find the median of 37, 31, 42, 43, 46, 25, 39, 45, 32.

11. Find the mode of the following series. 25, 23, 22, 22, 24, 27, 27, 25, 23, 22, 26, 32.

12. If the median of a series of data is 3 and mean is 2 then, find the mode.

 Ans: 5

13. Find the median of the following data 19, 25, 59, 48, 35, 31, 30, 32, 51. If 25 is replaced by 52, what will be the new median. 

Ans: 32, 35

14. If the mean of the following distribution is 6, then find the value of p. 

$\begin{array}{*{20}{c}} {\mathbf{x}}&2&4&6&{10}&{p + {\mathbf{5}}} \\ {\mathbf{f}}&3&2&3&1&2 \\ \end{array}$

15. If the mean of five observations ${\text{x}},{\text{x}} + 2,{\text{x}} + 4,{\text{x}} + 6,{\text{x}} + 8$ is 11, find the mean of first three observation. 

Ans:   9

16. The mean of 5 numbers is 18. If one number is excluded, their mean is 16, find the excluded number.

Ans:   26

17. The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x.

$29,32,48,50,x,x + 2,72,78,84,95$

18. Find the value of x and y in the following distribution if it is known that the mean of the distribution is 1.46.

 Ans:  $x = 76,y = 38$

19. The mean monthly salary of 10 members of a group is Rs 1445 , one more member whose monthly salary is Rs 1500 has joined the group. Find the mean monthly salary of 11 members of the group. 

Ans: Rs 1450

20. Given below is a cumulative frequency distribution table showing the age of people living in a locality.

Prepare a frequency distribution table.

Ans: $\begin{array}{*{20}{c}} {{\text{ Marks }}}&{0 - 12}&{12 - 24}&{24 - 36}&{36 - 48}&{48 - 60}&{60 - 72}&{72 - 84}&{84 - 96}&{96 - 108} \\ {{\text{ Person }}}&{98}&{217}&{382}&{269}&{138}&{15}&2&2&1 \\ \end{array}$

21. If ${\mathbf{x}},{{\mathbf{x}}_2} \ldots ..{{\text{x}}_{\text{n}}}$ are ${\mathbf{n}}$ values of a variable x such that $\sum\limits_{i = 1}^n {\left( {{x_1} - 2} \right)}  = 110$ and $\sum\limits_{i = 1}^n {\left( {{x_1} - 5}\right)}  = 20$ find the value of n and mean.

Ans:  $\sum\limits_{i = 1}^n {\left( {{x_1} - 2} \right)}  = 110$

\[\Rightarrow \ \sum\limits_{i=1}^{n}{{{x}_{1}}-\ \ 2n}\text{ }\!\!~\!\!\text{ }=110\]

\[\Rightarrow \ \sum\limits_{i=1}^{n}{{{x}_{1}}=\ \ 2n}\text{ }\!\!~\!\!\text{ +}110\]

$\sum\limits_{i = 1}^n {\left( {{x_1} - 5} \right)}  = 20$

\[\Rightarrow \ \sum\limits_{i=1}^{n}{{{x}_{1}}-\ \ 5n}\text{ }\!\!~\!\!\text{ }=20\]

\[\Rightarrow \ \sum\limits_{i=1}^{n}{{{x}_{1}}=\ \ 5n}\text{ }\!\!~\!\!\text{ +20}\]

\[\Rightarrow \ 5n~+20\ =\ 2n\ +\ 110\]

\[ \Rightarrow 3n = 90 \]

\[ \Rightarrow  n=30 \]

\[\Rightarrow \ \bar{x}=\ \dfrac{\sum\limits_{i=1}^{n}{{{x}_{1}}}}{n}\text{ }\!\!~\!\!\text{ =}\ \dfrac{2n+110}{n}\ =\ \dfrac{2(30)\,\ +110}{30}\ =\ \dfrac{170}{30}\ =\ \dfrac{17}{3}\]

n $= 30$, mean $= \;\dfrac{{17}}{3}$

22. The mean of 200 items was 50. Later on, it was discovered that the two items were misread as 92 and 8 instead of 192 and 88. Find the correct mean.

\[ \bar{x}\ =\ \dfrac{\sum\limits_{i=1}^{n}{{{x}_{i}}}}{n}\  \]

\[ \Rightarrow \ 50\ =\ \dfrac{\sum\limits_{i=1}^{n}{{{x}_{i}}}}{200} \]

\[ \Rightarrow \ \sum\limits_{i=1}^{n}{{{x}_{i}}}\ =\ 200\ \times \ 50\ =\ 10000 \]

For new mean,

\[ \Rightarrow \ \sum\limits_{i=1}^{n}{{{x}_{i}}}\ =\ 10000-\ (92\ +\ 8)\ +\ (192\ +\ 88)\ \ =\ 10180 \]

\[ \Rightarrow \ \bar{x}\ =\ \dfrac{\sum\limits_{i=1}^{n}{{{x}_{i}}}}{n}\ =\ \dfrac{10180}{200}\ =\ 50.9 \]

23. Find the value of p, if the mean of the following distribution is 20 . 

$\begin{array}{*{20}{c}} {\text{x}}&{15}&{17}&{19}&{20 + {\text{p}}}&{23} \\ {{\text{ frequency }}}&2&3&4&{5{\text{p}}}&6 \\ \end{array}$

Ans:  1

Important Questions

1 marks questions.

3. If the ratio of mean and median of a certain data is 2: 3, then find the ratio of its

mode and mean.

7. Find the range of the following data: 25, 20, 30, 18, 16, 15.

Ans: (a) 15

8. Find the median of the given data: 7, 8, 7, 7, 9, 10, 13.

9. Find the mode of the given data: 7, 9, 11, 13, 9, 13, 9, 9, 7, 8.

10. Find the mean of the first five multiples of 3?

(d) None of these

11. The mean of 7 observations is 20. If the mean of the first 4 observations is 12 & that of last 4 observations is 28, find the ${4^{{\text{th }}}}$observation ?

Ans:   Since mean of 7 observations $ = 20$

$\therefore $ Total of 7 observations $ = 20 \times 7 = 140$

$\therefore $ Mean of first 4 observations $ = \;12$ $ \Rightarrow $ Total of first 4 observations $ = 12 \times 4 = 48$

$\therefore $ Mean of last 4 observations $ = \;28$ $ \Rightarrow $ Total of first 4 observations $ = 4 \times 28 = 92$

$\therefore $ Total of 7 observations $ + {4^{{\text{th }}}}$ observation $ = 48 + 92$

$140 + {4^{{\text{th }}}}$ observation  $ = 140$

$ \Rightarrow {4^{{\text{th }}}}$ observation  $ = 140 - 140 = 0$

12. What is the upper limit of the interval: $20 - 23?$

Ans: (b) 23

13. What is class size of interval 10, 12, 14, 16, 18  ?

Ans:   (a) 2

14. Find the class mark of the interval $15.7 - 25.7?$

Ans:   (a) 20.7

15. what is the mid-point of class interval $12.3 - 22.3\;?$

Ans:   (a) 17.3

16. The median of the following observations arranged in ascending order is 40. find x $15,\;12,\;11,\;14,\;x + 2,\;x + 4,\;32,\;30,\;41,\;35$

Ans:   No. of observation $ = 10$ which is even 

$\therefore $ Median is the average of ${\left( {\dfrac{n}{2}} \right)^{th}}\;\& \;{\left( {\dfrac{n}{2} + 1} \right)^{th}}$ abservations

So, ${5^{{\text{th }}}}$ observation $ = x + 2$ and ${6^{{\text{th }}}}$ observation $ = x + 4$

Median $ = \dfrac{{(x + 2) + (x + 4)}}{2}$

$40 = \dfrac{{2x + 6}}{2}$

$40 = x + 3$

$\therefore x = 37$

17. What is the class Mark of the interval 15-20 ?

(D) none of these

Ans: (C) 17.5

18. What is the range of interval 15-20?

Ans:  (A) 5

19. What is the class - size of the interval 15-20?

20. Find out the mean of following data. 5,10,15,20,25,30.

Ans:   (B) 17.5

21. Find the arithmetic mean of first 6 natural numbers?

(d) none of these

Ans:  (a) 3.5

22. What is the mid-point of interval 3-6 ?

Ans: (b) 4.5

23. Find out the range of the following: 5, 10, 15, 20, 25, 30.

Ans: (a) 25

24. Find out the mode of the following: 5, 4, 3, 5, 6, 6, 6, 5, 4, 5, 5, 3, 2, 1.

(c) 5 

(d) none of these 

25. What is the class size of the intervals 10-20 ?

Ans: (a) 10

26. What is the upper class limit of the class 37-43 ?

Ans: (c) 43

27. What is the lower class limit of the class 37-43 ?

Ans: (a) 37

28. Find the median of the following data: 15, 35, 18, 26, 19, 25, 29, 20, 27, 30.

Ans: (a) 25.5

2 Marks Questions

1. The mean of 10 numbers is 20. If 5 is subtracted from every number, what will be the new mean?

Ans:  15

2. Find the mean of first 10 even natural no.

3. Calculate the mean for the following distribution. 

$\begin{array}{*{20}{c}} {\mathbf{x}}&{\mathbf{5}}&{\mathbf{6}}&7&{\mathbf{8}}&{\mathbf{9}} \\ {\mathbf{f}}&{\mathbf{4}}&{\mathbf{8}}&{{\mathbf{14}}}&{{\mathbf{11}}}&{\mathbf{3}} \\ \end{array}$

4. Find the median of 37, 31, 42, 43, 46, 25, 39, 45, 32.

5. Find the mode of following series. 25, 23, 22, 22, 24, 27, 27, 25, 23, 22, 26, 32.

6. If the median of a series of data is 3 and mean is 2 then, find the mode.

7. If the mean of 5 observation ${\text{x}},{\text{x}} + 4,{\text{x}} + 8,{\text{x}} + 12,{\text{x}} + 16$ is 13, find the mean of the observations?

Ans: $\bar x = \dfrac{{{{\sum x }_i}}}{n}$

$ \Rightarrow 13 = \dfrac{{x + (x + 4) + (x + 8) + (x + 12) + (x + 16)}}{5}$

$ \Rightarrow 5 \times 13 = 5x + 40$

$ \Rightarrow 13 = x + 8$

$\therefore x = 5$

$\therefore $ The five given observations are 5, 9, 13, 17, 21 

$\bar x = \dfrac{{5 + 9 +  + 13 + 17 + 21}}{5} = 12.8$

8. The class marks of the observations are 17, 21, 25, 29, 33, 37, 41, 45. Find the class intervals.

Ans:  Class marks are 17, 21, 25, 29, 33, 37, 41  and 45 

Class size $ = \;21 - 17\; = \;25 - 21\; = \;4$  

Half of class size $ = \dfrac{4}{2} = 2$

Thus, Class intervals are:

9. The value of $\pi $ up to 15 decimal places is: $3.419078023195679$

(i) List the digits from 0 to 9 & make frequency distributions of the digit after the decimal points.

(ii) What are the most and the least frequently occurring digits?

Ans:  (i) Frequency distribution table

(ii) Most frequency occurring digits $ = \;9$  

Least frequently occurring digits $ = \;2,\;3,\;4,\;5,\;6,\;8$

10. A random survey of the number of children of various age group playing in the park was found:

$\begin{array}{*{20}{c}} {{\text{Age}}[{\text{in years}}]}&{1 - 2}&{2 - 3}&{3.5}&{5 - 7}&{7 \cdot 10} \\ {{\text{ No}}{\text{. of children }}}&3&5&7&{10}&{13} \\ \end{array}$

Draw a histogram to represent the data above?

Ans:  we will calculate the adjusted frequencies [AF] for histogram because the class intervals are not of equal width.

Minimum class size [CS] = 1

To get the required histogram, draw rectangles with base equal to class interval and heights equal to the corresponding adjusted frequencies.

(Image will be uploaded soon)

11. The mean of $20,\;8,\;12,\;13,\;15\;{\text{\& }}\;P$ is 30 . Find the value of $P$ ?

Ans . Mean $ = \bar x = \dfrac{{20 + 8 + 12 + 13 + 15 + P}}{6}$

$30 = \dfrac{{68 + P}}{6}$

$ \Rightarrow 180 = 68 + P$

$\therefore P = 180 - 68 = 112$

12. Find the mode of the following data: 14, 25, 14, 14, 25, 24, 20, 28, 18, 20.

Ans:   Arrange the given data in ascending order:

14, 14, 14, 18, 20, 20, 24, 25, 25, 28

The value 14 occurs most frequently i.e. 3 times as observed.

So, Mode is 14

13. Find the median of 5, 7, 10, 9, 5, 12, 15, 12, 18, 20. If 9 is replaced by 14, what will be the new median?

Ans:   Arrange the given data in ascending order: 

5, 5, 7, 9, 10, 12, 15, 18, 20

Here, ${\text{n}} = 10$ [even number]

So, Median $ = \dfrac{{{5^{{\text{th }}}}{\text{ observation }} + {6^{{\text{th }}}}{\text{ observaiton }}}}{2} = \dfrac{{10 + 12}}{2} = 11$

After replacing 9 by 14:

5, 5, 7, 10, 12, 12, 14, 15, 18, 20

Now, ${5^{{\text{th }}}}$ observation $ = {6^{{\text{th }}}}$ observation  $ = 12$

So, New Median $ = \dfrac{{12 + 12}}{2} = 12$

14. The average mark of boys in an examination is 68 & that of girls in 89. If the average mark of all candidates in that examination is 80 , find the ratio of the no. of boys to the number of girls that appeared in the examinations.

Ans:  Let number of boys be $x$ &  girls be y .

$\therefore $ Total marks of boys $ = 68 \times x = 68{\text{x}}$

$\therefore $ Total marks of girls $ = 89 \times y = 89y$

Hence, total marks for boys & girls $ = \;68x + 89y$

Also, total of boys &  girls $ = x + y$ &  average for all the candidates $ = 80$

$ \Rightarrow \;\;80\; = \;\dfrac{{68x + 89y}}{{x\; + \,y}}$

$80x + 80y = 68x + 89y$

$80x - 68x = 89y - 80y$

$ \Rightarrow \;\dfrac{x}{y} = \dfrac{9}{{12}} = \dfrac{3}{4}$

$\therefore $ Ratio of boys &  girls $ = 3:4$

15. The mean of 6 numbers is 30. If one number is excluded, their mean is 24. Find the excluded number.

Ans:  Here, ${\text{n}} = 6\;,\;\;\bar x = 30$

$\therefore \;\;\overline x  = \dfrac{1}{n}\left( {\sum {{x_i}} } \right)\; \Rightarrow \;\sum {{x_i}}  = n\overline x $

$\sum {{x_i}}  = 6 \times 30 = 180$

So, total of 6 numbers $ = 180$

Let the excluded number be a. 

Now, total of 5 number is 180 -a

Mean of 5 number $ = \dfrac{{180 - a}}{5}$

$ \Rightarrow 24 = \dfrac{{180 - a}}{5}$

$ \Rightarrow 24 \times 5 = 180 - a$

$ \Rightarrow a = 180 - 120$

$ \Rightarrow a = 60$

Thus, excluded number is 60.

16. The median of the observation  $11,\;12,\;14,\;18,\;x + 2,\;x + 4,\;30,\;32,\;35,\;41$, arranged in ascending order is 24 . find the value of x.

Ans:  Number of observation, ${\text{n}}\;{\text{ = }}\;10$

Since ${\text{n}}$ is even,

$\therefore $ median $ = \dfrac{{{{\left[ {\dfrac{n}{2}} \right]}^{th}}{\text{observation }} + {{\left[ {\dfrac{n}{2} + 1} \right]}^{th}}{\text{ observation }}}}{2}$

$ \Rightarrow 24 = \dfrac{{{5^{th}}{\text{observation }} + {6^{th}}{\text{ observation }}}}{2}$

$ \Rightarrow 24 = \dfrac{{(x + 2) + (x + 4)}}{2}$

$ \Rightarrow 24 = \dfrac{{2x + 6}}{2} \Rightarrow 24 = x + 3$

$ \Rightarrow x = 21$

So, ${\text{x}} = 21$

17. Find the median of the following data: 25, 34, 31, 23, 22, 26, 35, 28, 20, 32.

Ans:  Arrange the data in ascending order:

20, 22, 23, 25, 26, 28, 31, 32, 34, 35.

Hence, the no. of observation $n\; = \;10$   (even)

$ \Rightarrow \;{\text{median}}\; = \dfrac{{{5^{th}}{\text{observation }} + {6^{th}}{\text{ observation }}}}{2}$

$ = \dfrac{{26 + 28}}{2} = 27$

So, median of the data is 27 .

18. In x standard, these are three sections A, B, C with 25, 40 and 30 students respectively. The average mark of section A is $70\% $, of section B is $65\% $ and of section B is $50\% $. Find the average marks of the entire X standard.

Ans: ${n_1} = 25,{n_2} = 40,{n_3} = 35$

${\bar x_1} = 70,{\bar x_2} = 65$ , and ${\overline x _3} = 50$

Let $\overline X $ , denote the average mark of the entire X standard. 

Then, $\bar X = \dfrac{{{n_1}{{\bar X}_1} + {{\text{n}}_2}{{\bar X}_2} + {{\text{n}}_3}{{\bar X}_3}}}{{{n_2} + {{\text{n}}_2} + {{\text{n}}_3}}}$

$ = \dfrac{{25 \times 70 + 40 \times 65 + 35 \times 50}}{{25 + 40 + 35}}$

$ = \dfrac{{1750 + 2600 + 1750}}{{100}}$

$ = \dfrac{{6100}}{{100}} = 61$

So, the average marks of the entire X standard is $61\% $ .

19. If $\bar x$ is a mean of ${x_1}{\text{,}}\;{{\text{x}}_2},\;{{\text{x}}_3} -  -  -  -  -  - {{\text{x}}_n}$ then the mean of $a{x_1},\;a{x_2},\; -  -  -  - ,\;a{x_n}$ is $a\bar x$ where ‘a’ is any number different from 2 era i.e. if each observation is multiplied by a non 2 era number a, then the mean is also multiplied by a.

Ans:  We have: $\bar X = \dfrac{1}{n}\left[ {\sum\limits_{i = 1}^n {{X_i}} } \right]$

Let $X$ be the mean of $a{x_1},a{x_2} \ldots .a{x_n}$ . Then,

$X = \dfrac{{a{x_1} + a{x_2} +  \ldots  + a{x_n}}}{n}$

$ = \dfrac{{a\left( {{{\text{x}}_1} + {{\text{x}}_7} +  \ldots  \ldots  + {{\text{x}}_n}} \right)}}{n}$

$ = {\text{a}}\left[ {\dfrac{1}{n}\sum\limits_{i = 1}^n {{X_i}} } \right]$

$ = a\overline X $

Thus, mean gets multiplied by a.

20. The class marks of a distribution are 26, 31, 41, 36, 46, 51, 56, 61, 66, 71. Find the true class limits.

Ans:  Class size is the difference between any two consecutive class marks because class marks are uniformly spaced.

$\therefore $ Class size $ = 31 - 26 = 5$

If a is the class mark of a class interval of size $h$ , then the lower and upper limits of the class intervals are $a - \dfrac{h}{2}$ and $a + \dfrac{n}{2}$ respectively .

Here ${\text{h}} = 5$

$\therefore $ Lower limit of first class interval $ = 26 - \dfrac{5}{2} = 23.5$ and upper limit of first class interval $ = 26 + \dfrac{5}{2} = 28.5$

$\therefore $ First class interval is 23.5-28.5

So, true class limits:

$23.5 - 28.5,\;\;28.5 - 33.5,\;\;33.5 - 38.5,\;\;38.5 - 43.5,\;\;43.5 - 48.5,\;\;48.5 - 53.5$

21. The marks obtained by 15 students in an examination are given below;

125, 130, 130, 120, 141, 146, 162, 163, 169, 173, 179, 188, 192, 195, 199.

Form a cumulative frequency table with class interval of length 20.

22. For the following data, draw a histogram and a frequency polygon.

23. If $X$ is the mean of $n$ observation ${x_1},{{\text{x}}_2} \ldots  \ldots ,{x_n}$, then prove that the mean of ${x_1} - a,\;{x_2} - a \ldots ..,\;{x_n} - a$, is $X - a$, where a is any real number.

Ans:  We have $\bar X = \dfrac{1}{n}\left[ {\sum\limits_{i = 1}^n {{X_t}} } \right]$  

Let $X$ be the mean of  ${x_1} - {a_2},\;{x_2} - a,... \ldots ,\;{x_3} - a$ . 

Then, $X = \dfrac{{\left( {{x_1} - a} \right) + \left( {{x_2} - a} \right) +  \ldots . + \left( {{x_n} - a} \right)}}{n}$

$ = \dfrac{{\left( {{x_1} + {x_1} +  \ldots .{x_n}} \right) - na}}{n}$

$ = \dfrac{1}{n}\left[ {\sum\limits_{i = 1}^n {{X_t}} } \right] - \dfrac{{na}}{a}$

$ = \bar X - a\quad $

Hence, proved.

24. The mean of 16 numbers is 8. If 2 is added to every number, what will be new mean?

Ans:  Let ${{\text{x}}_1},{{\text{x}}_2}{{\text{x}}_3} \ldots  \ldots ,{x_{16}}$ be 16 numbers with their mean equal to 8 . 

Then, $\bar X = \dfrac{1}{n}\left( {\sum {{x_i}} } \right)$

$ \Rightarrow 8 = \dfrac{{{x_1} + {x_2} +  \ldots .. + {x_{15}}}}{{16}}$

$ \Rightarrow 16 \times 8 = {x_1} + {x_2} +  \ldots  \ldots  + {x_{16}}$

New numbers are : ${x_1} + 2,\;{{\text{x}}_2} + 2,\;{{\text{x}}_3} + 2,\; \ldots  \ldots ,\;{x_{16}} + 2$

Let $X$ Be the mean of new numbers. Then,

$X = \dfrac{{\left( {{x_1} + 2} \right) + \left( {{x_2} + 2} \right) +  \ldots .. + \left( {{x_{16}} + 2} \right)}}{{16}}$

$ = \dfrac{{\left( {{x_1} + {x_2} +  \ldots  \ldots  + {x_{16}}} \right) + 2 \times 16}}{{16}}$  

$ = \dfrac{{128 + 32}}{{16}}$

$ = \dfrac{{160}}{{16}} = 10$

25. Calculate the mean from the given data.

${\sum f _i} = n = 60$   and   ${\sum f _i}{x_i} = 1715$

$\therefore $ mean $ = \dfrac{{{{\sum f }_i}{x_i}}}{n} = \dfrac{{1715}}{{60}} = 28.5$

26. The following table gives the mark scored by 50 students in an entrance examination:

From this table find:

(i) the less than series and

(ii) the more than series.

Ans: (i) Less than cumulative frequency table.

(ii) More than cumulative frequency table.

27. Find the sum of the deviations of the various values 3, 4, 6, 8, 14  from their mean.

Ans:  Recall that the deviations of the values ${{\text{x}}_1},{{\text{x}}_2},{{\text{x}}_3} \ldots  \ldots .{{\text{x}}_{\text{n}}}$ about ${\text{A}}$ are

${{\text{X}}_1} - {\text{A}},\;\;{{\text{x}}_2} - {\text{A}},\;\;{{\text{x}}_3} - {\text{A,}}\;\; \ldots  \ldots  \ldots .,\;{{\text{x}}_{\text{n}}} - {\text{A}}$

Let $X$ be the deviations of the values 3, 4, 6, 8, 14. Then,

$X = \dfrac{{3 + 4 + 6 + 8 + 14}}{5} = \dfrac{{35}}{5} = 7$

Now, sum of the deviations of the values 3, 4, 6, 8 and 14 , From their mean $\overline X  = 7$ is given by 

$(3 - 7) + (4 - 7) + (6 - 7) + (8 - 7) + (14 - 4) =  - 4 - 3 - 1 + 1 + 7 = 0$

28. The mean of 40 observations was 200 . It was detected on rechecking that the value of 65 was wrongly copied as 25 for computation of mean. Find the correct mean.

Ans:   ${\text{n}} = 40,\;\;\overline X  = 200$

So, $X = \dfrac{1}{n}\left( {\sum x } \right) \Rightarrow 200 = \dfrac{1}{{40}}\left( {\sum {{x_i}} } \right)$

$\sum {{x_1}}  = 200 \times 40 = 8000$

$\therefore $ Incorrect value of $\sum x  = 8000$

correct value of $\sum {{x_i}}  = $ incorrect value of $\sum {{x_1}} $ -  incorrect item + correct item $ = 8000 - 25 + 65\;\; = \;\;8040$

$\therefore $ correct mean $ = \dfrac{{8040}}{{40}} = 201$

29. It $\overline X $ is the mean of n observation ${x_1},\;{x_2}, \ldots  \ldots .,\;{x_2}$, then prove that $\sum\limits_{i = 1}^n {\left( {{X_t} - \overline X } \right)}  = 0$

i.e., the algebraic sum of deviations from mean is zero.

Ans:  We have $\bar X = \dfrac{1}{n}\left[ {\sum\limits_{i = 1}^n {{x_i}} } \right]$

$ \Rightarrow {\text{n}}\bar X = \sum\limits_{{\text{l}} = 1}^n {{x_i}} $

Now, $\sum\limits_{{\text{i}} = 1}^n {\left( {{x_{\text{i}}} - \bar X} \right)}  = \left( {{x_i} - \bar X} \right) + \left( {{x_2} - \bar X} \right) +  \ldots . + \left( {{{\text{x}}_n} - \bar X} \right)$

$ = \left( {{x_1} + {x_2} +  \ldots . + {x_n}} \right) - n\overline X $

$ = \sum\limits_{{\text{i}} - 1}^n {{x_{\text{i}}}}  - n\bar X$

$ = \;n\overline X \; - \;n\overline X $

So, $\sum\limits_{i = 1}^n {\left( {{x_i} - \bar X} \right)}  = 0$

3 Marks Questions

1. Find the median of the following data 19, 25, 59, 48, 35, 31, 30, 32, 51. If 25 is replaced by 52, what will be the new median. 

2. If the mean of the following distribution is 6, then find the value of p.

3. If the mean of five observations ${\text{x}},{\text{x}} + 2,{\text{x}} + 4,{\text{x}} + 6,{\text{x}} + 8$ is 11, find the mean of first three observation. 

4. The mean of 5 numbers is 18. If one number is excluded, their mean is 16, find the excluded number.

5. The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x.

6. (i) Find the mean of the following data: 25, 27, 19, 29, 21, 23, 25, 30, 28, 20.

Show that the sum of deviation of all the observations from the mean is zero.

(ii) Find the median of the data given above.

Ans:  (i) Mean $ = \;\bar x = \dfrac{{25 + 27 + 19 + 29 + 21 + 23 + 25 + 30 + 28 + 20}}{{10}} = \dfrac{{247}}{{10}} = 24.7$

Sum of the deviations of all the observations from the mean $ = \sum\limits_{i = 1}^{10} {(x - \bar x)} $

$ = (25 - 24.7) + (27 - 24.7) + (19 - 24.7) + (27 - 24.7) + $

$(23 - 24.7) + (25 - 24.7) + (30 - 24.7) + (28 - 24.7) + (20 - 24.7)$

$ = 0.3 + 2.3 - 5.7 + 4.3 - 2.7 - 1.7 + 03 + 5.3 + 3.3 - 4.7 = 0$

(ii) Arranging the data in ascending order: $19,20,21,23,25,25,27,28,29,30$

$\therefore $ Median $ = \;\;\dfrac{{{{\left[ {\dfrac{n}{2}} \right]}^{[th}}{\text{observation }} + {{\left[ {\dfrac{n}{2} + 1} \right]}^{th}}{\text{observation }}}}{2}$

$ = \dfrac{{{5^{{\text{th }}}}{\text{observation }} + {6^{{\text{th }}}}{\text{observation }}}}{2} = \dfrac{{25 + 25}}{2} = 25$

7. If the mean of the following data is 21 . Find the value of ${\text{P}}$.

X   7  15  28  5  1

Y   8  20   P   3  2

$\sum {{f_i}}  = 33 + P\quad \sum {{x_i}} {f_i} = 373 + 28P$

$\bar x = \dfrac{{\sum {{x_1}} {f_f}}}{{\sum {{f_i}} }}$

$21 = \dfrac{{373 + 28P}}{{33 + P}}$

$21 \times 33 + 21P = 373 + 28P$

$693 + 21P = 373 + 28P$

$693 - 373 = 28P - 21P$

$P = \dfrac{{320}}{7}$

$\therefore P = 45.7$

8. In a mathematics test given to 10 students, the following marks [out of 100] are recorded as: 82, 41, 39, 52, 53, 45, 96, 47, 50, 60.

Find out the mean & median of the above marks.

Ans:  The given observation are:  82, 41, 39, 52, 53, 45, 96, 47, 50, 60

Sum of 10 observations $ = 82 + 41 + 39 + 52 + 53 + 45 + 96 + 47 + 50 + 60\; = \;565$

$\bar X = \dfrac{1}{n}\left[ {\sum\limits_{i = 1}^n {{x_i}} } \right]$

$\therefore \;\;\overline X \; = \dfrac{{565}}{{10}} = 56.5$

Arrange given observation in ascending order:

39, 41, 45, 47, 50, 52, 53, 60, 82, 96.

Here,  n = 10  [even no.]

$\therefore $ Median $ = \dfrac{{{{\left( {\dfrac{n}{2}} \right)}^{{\text{th }}}}{\text{observation }} + {{\left( {\dfrac{n}{2} + 1} \right)}^{th}}{\text{observation }}}}{2}$

$ = \dfrac{{{5^{{\text{th }}}}{\text{observation }} + {6^{{\text{th }}}}{\text{observation }}}}{2}$

$ = \dfrac{{50 + 52}}{2} = \dfrac{{102}}{2} = 51$

9. The following is the monthly expenditure (Rs.) of ten families of the particular area:

145, 115, 129, 135, 139, 158, 170, 175, 188, 163

(a) Make a frequency distribution table by using the following class interval:

100-120,  120-140,  140-160,  160-180,  180-200.

(b) Construct a frequency polygon for the above frequency distribution.

10. The mean of 5 numbers is 39.  If one number is excluded, their mean is 35 , find the excluded number.

Ans: The mean of 5 numbers $ = 39$

So, sum of five numbers $ = 39 \times 5 = 195$

The mean of 4 numbers $ = 35$

So, sum of four numbers $ = 35 \times 4 = 140$

Thus,  Excluded numbers = Sum of five numbers - Sum of four numbers

$ = 195 - 140 = 55$

11. If the mean of 8 observation $x,\;x + 1,\;x + 3,\;x + 4,\;x + 5,\;x + 6,\;x + 7$ is 50, find the mean of  first 5 observation.

Ans: Mean $ = \dfrac{{\sum {{x_i}} }}{n}$

$\bar x = \dfrac{{x + (x + 1) + (x + 2) + (x + 3) + (x + 4) + (x + 5) + (x + 6) + (x + 7)}}{8}$

$50 = \dfrac{{8x + 28}}{8}$

$400 - 28 = 8x$

$\therefore x = \dfrac{{372}}{8} = 46.5$

The given set of 8 observations is 46.5, 47.5, 48.5, 50.5, 49.5, 51.5, 52.5, 53.5.

So, mean of first 5 observations is:

$\bar x = \dfrac{{46.5 + 47.5 + 48.5 + 49.5 + 50.5}}{5} = \dfrac{{242.5}}{5} = 48.5$

12. Represent the following data by means of histogram.

Following will be the adjusted Frequencies:

13. The Mean of monthly salary of 10 members of a group is Rs 1445, one more member whose monthly salary is Rs 1500 has joined the group. Find mean monthly salary of 11 member of the group.

Ans:   Here $n = 10,\;\;\bar X = 1445$

So, $\bar X = \dfrac{1}{n}\left( {\sum {{x_i}} } \right) \Rightarrow {\text{n}}\bar X = \sum {{x_i}}  \Rightarrow 10 \times 1445 = \sum {{x_i}} $

$ \Rightarrow \sum {{x_i}}  = 14450$

So, total monthly wages of 10 person ${\text{Rs}} = 14450$

Monthly salary wages of one more person who joined the group is 1500 .

$\therefore $ Total monthly wages of 11 persons = Rs $14450 + 1500 = $ Rs 15950

So, average monthly salary to 11 person

$ = \dfrac{{{\text{ total monthly wages }}}}{{11}} = \dfrac{{15950}}{{11}} = \operatorname{Rs} 1450$

14. The sum of the deviations of a set of n values ${{\text{x}}_1},\;{{\text{x}}_2},\;..........\;{{\text{x}}_n}$ measured from 50 is  -10 and the sum of deviation of the values from 46 is 70. Find the values of ${\text{n}}$ and the mean.

Ans:  We have,

$\sum\limits_{i = 1}^n {\left( {{x_i} - 50} \right)}  =  - 10$ and  $\sum\limits_{i = 1}^n {\left( {{x_i} - 46} \right)}  = 70$

$ \Rightarrow \sum\limits_{i = 1}^n {{x_i}}  - 50n = 10 \to $ (i)

$ \Rightarrow \sum\limits_{i = 1}^n {{x_i}}  - 46n = 70 \to $ (ii)

Subtracting  (ii) from (i), we get $ - \;4{\text{n}} =  - \;80$

${\text{n}} = 20$

Putting ${\text{n}} = 20$ in (i), we get

$\sum\limits_{i = 1}^n {{x_i} - 50 \times 20 = \;\; - 10} $

$ \Rightarrow \sum\limits_{{\text{l}} = 1}^n {{X_i}}  = 990$

$\therefore $ mean $ = \dfrac{1}{n}\left[ {\sum\limits_{i = 1}^n {{x_i}} } \right] = \dfrac{{990}}{{20}}$ $ = \,\;49.5$

So,  ${\text{n}} = 20$ and mean $ = 49.5$

15. There are 50 students in a class out of which 40 are boys and rest girls. The average weight of the class is 44 kg and the average weight of the girls is40 kg. Find the average weight of the boys.

Ans:   We have, n = No. of students in a class $ = 50$

${{\text{n}}_1} = $ No. of boys in a class $ = 40$

${{\text{n}}_2} = $ No. of girls in a class $ = 10$

${\bar X_1} = $ Average weight of boys $ = ?$

${X_2} = $ Average weight of girls $ = 40\;{\text{kg}}$

$\therefore \bar X = \dfrac{{{n_1}{{\bar X}_1} + {n_2}{{\bar X}_2}}}{{{n_1} + {n_2}}}$

$ \Rightarrow 44 = \dfrac{{40{{\overline X }_1} + 10 \times 40}}{{40 + 10}}$

$ \Rightarrow 50 \times 44 = 40{\overline X _1} + 400$

$ \Rightarrow 2200 = 40{\bar X_1} + 400$

$ \Rightarrow {\bar X_1} = 45$

Hence, the average weight of boys is $45{\text{Kg}}$

16. The mean of 100 items was found to be 300. If at the time of calculation two items were wrongly taken as 32 and 12 instead of 23 and 11 , find the correct mean.

Ans: Here, ${\text{n}} = 100,\quad X = 30$

So, $\overline X  = \dfrac{1}{n}\left( {\sum {{x_i}} } \right) \Rightarrow \sum {{x_i}}  = n\bar X$

$ \Rightarrow \sum {{x_i}}  = 100 \times 30$ $ = 3000$

$\therefore $ Incorrect value of $\sum {{x_i}}  = 3000$

Now, correct value of $\sum {{x_i}}  = $ incorrect value of $\sum {{x_i}}  - ($ sum of incorrect value $) + ($ sum of correct value)

  $ = 3000 - (32 + 12) + (23 + 11)\;\; = \;2990$

Correct mean $ = \dfrac{{{\text{ Correct value of }}\sum {{x_i}} }}{n} = \dfrac{{2990}}{{100}}$ $ = \;\;29.9$

17. The mean of 10 numbers is 20 . If 8 is subtracted from every number, what will be the new mean?

$\bar X = \dfrac{1}{n}\left( {\sum {{x_i}} } \right)$

$20 = \dfrac{{{x_1} + {x_2} +  \ldots .. + {x_{20}}}}{{10}}$

$ \Rightarrow 200 = {{\text{x}}_1} + {x_2} +  \ldots . + {x_{10}}$

New numbers are ${x_1} - 8,\;{x_2} - 8,\; \ldots  \ldots ,\;{x_{10}} - 8$

$\overline X  = \dfrac{{\left( {{x_1} - 8} \right) + \left( {{x_2} - 8} \right) +  \ldots . + \left( {{x_{10}} - 8} \right)}}{{10}}$

$X = \dfrac{{\left( {{x_1} + {x_2} +  \ldots  \ldots  + {x_{10}}} \right) - 8 \times 10}}{{10}}$

$ = \dfrac{{200 - 80}}{{10}} = 12$

18. The mean of n observation ${x_1},\;{x_2},\;.......,\;{x_n}$, is $\overline X $. If $(a - b)$ is added to each of the observation, show that the mean of the new set of observation is $\overline X  + (a - b)$.

Ans:   We have,  $\bar X = \dfrac{{{x_1} + {x_1} +  \ldots  + {x_n}}}{n} \to $ (i)

Let $X$ be the mean of ${x_1} + (a - b),\;{x_2} + (a - b), \ldots  \ldots ,\;{x_n} + (a - b)$ . Then, $X = \dfrac{{\left[ {{x_1} + (a - b)} \right] + \left[ {{x_2} + (a - b)} \right] +  \ldots  \ldots  + \left[ {{x_n} + (a - b)} \right]}}{n}$

$ = \dfrac{{{x_1} + {x_2} +  \ldots  + {x_n} + n(a - b)}}{n}$

$ = \dfrac{{{x_1} + {x_2} +  \ldots  + {x_n}}}{n} + \dfrac{{n(a - b)}}{n}$

$ = X + (a - b)$   [using (i)]

19. If ${{\text{x}}_1},{{\text{x}}_2} \ldots  \ldots {{\text{x}}_{\text{n}}}$ are n values of a variable X such that $\sum\limits_{i = 1}^n {\left( {{x_{\text{i}}} - 2} \right)}  = 110$ and $\sum\limits_{i = 1}^n {\left( {{x_1} - 5} \right)} .$ Find the value of  n and the mean.

Ans:  We have: $\sum\limits_{i = 1}^n {({x_i}}  - 2) = 110$ and $\sum\limits_{i = 1}^n {({x_i}}  - 5) = 20$

$ \Rightarrow \left( {{x_1} - 2} \right) + \left( {{x_2} - 2} \right) +  \ldots .. + \left( {{x_n} - 2} \right) = 110$

$ \Rightarrow \left( {{x_1} - 5} \right) + \left( {{x_2} - 5} \right) +  \ldots .. + \left( {{x_n} - 5} \right) = 20$

$ \Rightarrow \left( {{x_1} + {x_2} +  \ldots  + {x_n}} \right) - 2n = 110$ and $\left( {{x_1} + {x_2} +  \ldots  + {x_1}} \right) - 5n = 20$

$ \Rightarrow \sum\limits_{i = 1}^n {{x_i}}  - 2n = 110$ and $\sum\limits_{i = 1}^e {{x_1}}  - 5n = 20$

Thus, we have $S - 2n = 110$ ....(i)

and  $S - 5n = 20$ ....(ii)

Subtracting (ii) from (i), we get:

Putting ${\text{n}} = 30$ in (i), we get:

${\text{S}} - 60 = 110\;\; \Rightarrow \;{\text{S}} = 170 \Rightarrow \sum\limits_{{\text{i}} = 1}^n {{x_i}}  = 170$

$\therefore $ mean $ = \dfrac{1}{n}\left[ {\sum\limits_{i = 1}^n {{x_i}} } \right]$

$ = \dfrac{{170}}{{30}} = \dfrac{{17}}{3}$

20. Find the missing frequencies in the following frequency distribution shown that the mean of the distribution is 1.46.

Ans: Let the missing frequencies be f 1 and f 2 .

We have: ${\text{N}} = 200$

$\therefore 200 = 86 + {f_1} + {f_2}$

$114 = {f_1} + {f_2}.............({\text{i}})$

Also, Mean $ = 1.46$

$ \Rightarrow 1.46 = \dfrac{{\sum {{f_i}} {x_i}}}{N}$

$ \Rightarrow 1.46 = \dfrac{{140 + {f_1} + 2{f_2}}}{{200}}$

$ \Rightarrow 292 = 140 + {{\text{f}}_1} + 2{{\text{f}}_2}$

$ \Rightarrow 152 = {{\text{f}}_1} + 2{{\text{f}}_2}..........(ii)$

Solving (i) and (ii), we get

${{\text{f}}_1} = 76$ and ${{\text{f}}_2} = 38$

21. Give some examples of data that you can collect from your day to day life. 

Ans: Some examples of data that we can gather from our day to day life are:

Number of students in our college. 

Number of fans in our school library.

Electricity bills of our shop for last three years.

Election results obtained from television or newspapers. 

Literacy rate figures obtained from National Survey. 

 Heights of 30 students of our class.

 Maximum temperatures of the days of a particular week from weather forcast. 

Number of members in the families of your locality from a record.

 Distances from the college of the homes of five students.

22. Classify the data in Q21 above as primary or secondary data. 

Ans: Primary Data: When investigator himself collects the information with some specific objective in mind, data obtained is called Primary data. Such types of data are collected for first time for their own use. Above mentioned (i), (ii), (iii), (iv) and (ix) are the examples of primary data.

Secondary Data: It includes the collection of information from sources which already had the information stored such as newspaper, television, etc. Above mentioned (iv), (v), (vii) and (viii) are the examples of secondary data.

23. The blood groups of 30 students of a class VIII are recorded as follows: 

A,  B,  O,  O,  AB,  O,  A,  O,  B,  A,  O,  B,  A,  O,  O,  A,  AB,  O,  A,  A,  O,  O,  AB,  B,  A,  O,  B,  A,  B,  O .

Represent this data in the form of a frequency distribution table. Which is the most common and which is the rarest blood group among these students?

Ans: The frequency distribution table for the given data is as follows:

From the table, It can be  observed that the most common blood group is O and the rarest group is AB.

24. Distance (in km) of 40 engineers from their place of residence to their place of work were found as follows:

Construct a grouped frequency distribution table with class size 5 for the data given 40 above taking the first interval as 0 – 5 (5 not included). What main features do you observe from this tabular representation? 

Ans. The grouped frequency distribution table for the given data is as follows:

From the table we observe that out of 40 female engineers $36(5 + 11 + 11 + 9)$ engineers i.e. $90\% $ of the total female engineers reside less than $20\;{\text{km}}$ from their place of work.

25. The relative humidity (in %) of a certain city for a month of 30 days was as follows:

(i) Construct a grouped frequency distribution table with classes $84 - 86,86 - 88$ etc.

(ii) Which month or season do you think this data is about?

(iii) What is the range of this data?

Ans:   (i) The grouped frequency distribution table for the given data is as follows:

(ii) Data appears to be taken in the rainy season because we observe that relative humidity is high.

(iii) From the data, we observe 

Highest relative humidity $ = 99.2\% $

Lowest relative humidity $ = 84.9\% $

Range $ = \;\;(99.2 - 84.9)\%  = 14.3\% $

26. The heights of 50 students, measured to the nearest centimeters have been found to be as follows:

$\begin{array}{llllllllll} \mathbf{1 6 1} & \mathbf{1 5 0} & \mathbf{1 5 4} & \mathbf{1 6 5} & \mathbf{1 6 8} & \mathbf{1 6 1} & \mathbf{1 5 4} & \mathbf{1 6 2} & \mathbf{1 5 0} & \mathbf{1 5 1} \\ \mathbf{1 6 2} & \mathbf{1 6 4} & \mathbf{1 7 1} & \mathbf{1 6 5} & \mathbf{1 5 8} & \mathbf{1 5 4} & \mathbf{1 5 6} & \mathbf{1 7 2} & \mathbf{1 6 0} & \mathbf{1 7 0} \\ \mathbf{1 5 3} & \mathbf{1 5 9} & \mathbf{1 6 1} & \mathbf{1 7 0} & \mathbf{1 6 2} & \mathbf{1 6 5} & \mathbf{1 6 6} & \mathbf{1 6 8} & \mathbf{1 6 5} & \mathbf{1 6 4} \\ \mathbf{1 5 4} & \mathbf{1 5 2} & \mathbf{1 5 3} & \mathbf{1 5 6} & \mathbf{1 5 8} & \mathbf{1 6 2} & \mathbf{1 6 0} & \mathbf{1 6 1} & \mathbf{1 7 3} & \mathbf{1 6 6} \\ \mathbf{1 6 1} & \mathbf{1 5 9} & \mathbf{1 6 2} & \mathbf{1 6 7} & \mathbf{1 6 8} & \mathbf{1 5 9} & \mathbf{1 5 8} & \mathbf{1 5 3} & \mathbf{1 5 4} & \mathbf{1 5 9} \end{array}$

(i) Represent the data given above by a grouped frequency distribution table, taking the class - intervals as $160 - 165,165 - 170$ etc.

(ii) What can you conclude about their heights from the table?

Ans: (i) The grouped frequency distribution table for the given data is as follows:

(ii) From the frequency distribution table drawn above, we conclude that more than $50\% $ of the students are shorter than $165\;{\text{cm}}$ .

27. A study was conducted to find out the concentration of sulphur dioxide in the air in parts per million (ppm) of a certain city. The data obtained for 30 days is as follows:

$\begin{array}{llllll} 0.03 & 0.08 & 0.08 & 0.09 & 0.04 & 0.17 \\ 0.16 & 0.05 & 0.02 & 0.06 & 0.18 & 0.20 \\ 0.11 & 0.08 & 0.12 & 0.13 & 0.22 & 0.07 \\ 0.08 & 0.01 & 0.10 & 0.06 & 0.09 & 0.18 \\ 0.11 & 0.07 & 0.05 & 0.07 & 0.01 & 0.04 \end{array}$

(i) Make a grouped frequency distribution table for this data with class intervals as 

0.01 - 0.04, 0.04-0.08 and so on.

(ii) For how many days, was the concentration of sulphur dioxide more than 0.11  parts per million.

Ans: (i) The minimum and maximum concentration of Sulphur dioxide in the air in parts per million is 0.01 and 0.22 respectively.

It is given that 0.00-0.04 is one of the class intervals and the class size is the same.

So, the classes of equal size are

0.00-0.04, 0.04-0.08 , .. , 0.20-0.24

Thus, the frequency distribution table is as under.

$\begin{array}{|c|c|} \hline \begin{array}{c} \text { Concentration of } \\ \text { Sulphur dioxide (in ppm) } \end{array} & \text { Frequency } \\ \hline 0.00-0.04 & 4 \\ 0.04-0.08 & 9 \\ 0.08-0.12 & 9 \\ 0.12-0.16 & 2 \\ 0.16-0.20 & 4 \\ 0.20-0.24 & 2 \\ \hline \text { Total } & 30 \\ \hline \end{array}$

(ii) The concentration of sulphur dioxide was more than 0.11 ppm for 8 days.

28. Three coins were tossed 30 times simultaneously. Each time the number of heads occurring was noted down as follows:

$\begin{array}{*{20}{l}} 0&1&2&2&1&2&3&1&3&0 \\ 1&3&1&1&2&2&0&1&2&1 \\  3&0&0&1&1&2&3&2&2&0 \end{array}$

Prepare a frequency distribution for the data given above.

$\begin{array}{|c|c|} \hline \text { Number of heads } & \text { Number of times (frequency) } \\ \hline 0 & 6 \\ \hline 1 & 10 \\ \hline 2 & 9 \\ \hline 3 & 5 \\ \hline \text { Total } & 30 \\ \hline \end{array}$

29. The value of $\pi $ up to 50 decimal places is given below:

3.1415926535 8979323846 2643383279 5028841971 6939937510

(a) Make a frequency distribution of the digits after the decimal point and list the digits from 0 to 9 in your first column.

(b) What are the most and the least frequency occurring digits?

Ans: (i) The frequency distribution table is as under:

$\begin{array}{|c|c|} \hline \text { Digits } & \text { Frequency } \\ \hline 0 & 2 \\ 1 & 5 \\ 2 & 5 \\ 3 & 8 \\ 4 & 4 \\ 5 & 5 \\ 6 & 4 \\ 7 & 4 \\ 8 & 5 \\ 9 & 8 \\ \hline \text { Total } & 50 \\ \hline \hline \end{array}$

(ii) The most frequently occurring digits are 3 and 9. 

The least occurring is 0.

30. Thirty children were asked about the number of hours they watched TV programmers in the previous week. The results were found as follows: 

$\begin{array}{llllllllll} 1 & 6 & 2 & 3 & 5 & 12 & 5 & 8 & 4 & 8 \\ 10 & 3 & 4 & 12 & 2 & 8 & 15 & 1 & 17 & 6 \\ 3 & 2 & 8 & 5 & 9 & 6 & 8 & 7 & 14 & 12 \end{array}$

(i) Make a grouped frequency distribution table for this data, taking class width 5 and one of the class interval 5 – 10. 

(ii) How many children watched television for 15 or more hours a week?

Ans: (i) The minimum and maximum number of hours children watched TV programmers in the previous week are 1 hour and 17 hours, respectively. It is given that 5 – 10 is one of the class intervals and the class size is same. So, the classes of equal size are 0 – 5, 5 – 10, 10 – 15, 15 – 20. 

Thus, the frequency distribution table is as under. 

$\begin{array}{|c|c|} \hline \text { Number of heads } & \text { Frequency } \\ \hline 0-5 & 10 \\ 5-10 & 13 \\ 10-15 & 5 \\ 15-20 & 2 \\ \hline \text { Total } & 30 \\ \hline \end{array}$

(ii) 2 children watched television for 15 or more hours a week

31. A company manufactures car-batteries of particular type. The live (in years) of 40 such batteries were recorded as follows: 

$\begin{array}{llllllll} 2.6 & 3.0 & 3.7 & 3.2 & 2.2 & 4.1 & 3.5 & 4.5 \\ 3.5 & 2.3 & 3.2 & 3.4 & 3.8 & 3.2 & 4.6 & 3.7 \\ 2.5 & 4.4 & 3.4 & 3.3 & 2.9 & 3.0 & 4.3 & 2.8 \\ 3.5 & 3.2 & 3.9 & 3.2 & 3.2 & 3.1 & 3.7 & 3.4 \\ 4.6 & 3.8 & 3.2 & 2.6 & 3.5 & 4.2 & 2.9 & 3.6 \end{array}$

Construct a grouped frequency distribution table for this data, using class intervals of 45 size 0.5 starting from the interval 2 – 2.5.

Ans:   The minimum and maximum life (in number of years) of car batteries are 2.2 years and 4.6 years. It is given that 2 – 2.5 is one of the class interval with uniform size of 0.5. So, the classes of equal size are 2.0 – 2.5, 2.5 – 3.0, 3.0 – 3.5,……, 4.5 – 5.0.

Thus, the frequency distribution table is as under:

$\begin{array}{|c|c|} \hline \begin{array}{c} \text { Life of batteries } \\ \text { (in years) } \end{array} & \text { Frequency } \\ \hline 2.0-2.5 & 2 \\ 2.5-3.0 & 6 \\ 3.0-3.5 & 14 \\ 3.5-4.0 & 11 \\ 4.0-4.5 & 4 \\ 4.5-5.0 & 3 \\ \hline \text { Total } & 30 \\ \hline \end{array}$

4 Marks Questions

1. Find the value of x and y in the following distribution if it is known that the mean of the distribution is 1.46.

2. The mean monthly salary of 10 members of a group is Rs 1445 , one more member whose monthly salary is Rs 1500 has joined the group. Find the mean monthly salary of 11 members of the group. 

3. Given below is a cumulative frequency distribution table showing the age of people living in a locality.

$\begin{array}{l|l} \text { Age in years } & \text { No. of persons } \\ \hline \text { Above 108 } & 0 \\ \hline \text { Above 96 } & 1 \\ \hline \text { Above 84 } & 3 \\ \hline \text { Above 72 } & 5 \\ \hline \text { Above 60 } & 20 \\ \hline \text { Above 48 } & 158 \\ \hline \text { Above } 36 & 427 \\ \hline \text { Above 24 } & 809 \\ \hline \text { Above 12 } & 1026 \\ \hline \text { Above 0 } & 1124 \\ \hline \end{array}$

$\begin{array}{|l|l|l|l|l|l|l|l|l|l|} \hline \text { Marks } & 0-12 & 12-24 & 24-36 & 36-48 & 48-60 & 60-72 & 72-84 & 84-96 & 96-108 \\ \hline \text { Person } & 98 & 217 & 382 & 269 & 138 & 15 & 2 & 2 & 1 \\ \hline \hline \end{array}$

4. If ${\mathbf{x}},{{\mathbf{x}}_2} \ldots ..{{\text{x}}_{\text{n}}}$ are ${\mathbf{n}}$ values of a variable x such that $\sum\limits_{i = 1}^n {\left( {{x_1} - 2} \right)}  = 110$ and $\sum\limits_{i = 1}^n {\left( {{x_1} - 5} \right)}  = 20$ find the value of n and mean.

Ans:  n $ = 30$ , mean $ = \;\dfrac{{17}}{3}$

5. The mean of 200 items was 50. Later on, it was discovered that the two items were misread as 92 and 8 instead of 192 and 88. Find the correct mean.

6. Find the value of p, if the mean of the following distribution is 20 . 

$\begin{array}{|l|l|l|l|l|l|} \hline \mathrm{x} & 15 & 17 & 19 & 20+p & 23 \\ \hline \text { frequency } & 2 & 3 & 4 & 5 p & 6 \\ \hline \end{array}$

7. Prove that the sum of the deviations of an individual's observations from the mean is zero.

Ans:   Let ${{\text{x}}_1},{{\text{x}}_2},{{\text{x}}_3}, \cdots ,{{\text{x}}_{\text{n}}}$ be n  individual observations whose mean is $\bar x$ . The sum of the deviations of these n observations from $\overline x $ is given by:

$\sum\limits_{{\text{i}} = 1}^n {\left( {{x_{\text{i}}} - \overline x } \right)}  = \left( {{x_i} - \overline x } \right) + \left( {{x_2} - \overline x } \right) +  \ldots . + \left( {{{\text{x}}_n} - \overline x } \right)$

Also, we have $\overline x  = \dfrac{1}{n}\left[ {\sum\limits_{i = 1}^n {{x_i}} } \right]$

$ \Rightarrow {\text{n}}\overline x  = \sum\limits_{{\text{l}} = 1}^n {{x_i}} $

Now, $\sum\limits_{{\text{i}} = 1}^n {\left( {{x_{\text{i}}} - \overline x } \right)}  = \left( {{x_i} - \overline x } \right) + \left( {{x_2} - \overline x } \right) +  \ldots . + \left( {{{\text{x}}_n} - \overline x } \right)$

$ = \left( {{x_1} + {x_2} +  \ldots . + {x_n}} \right) - n\overline x $

$ = \sum\limits_{{\text{i}} - 1}^n {{x_{\text{i}}}}  - n\overline x $

$ = \;n\overline x \; - \;n\overline x $

So, $\sum\limits_{i = 1}^n {\left( {{x_i} - \overline x } \right)}  = 0$

8. From the data given below find: 

(a) Lower limit of the third class

(b) Upper limit of the seventh class.

(c) Class boundaries of the sixth class.

(d) The class mark of the fifth class.

(e) The size of the second class

(f) Draw histogram of the data.

$\begin{array}{|l|l|l|l|l|l|l|l|} \hline \text { No. of Wage[Rs.] } & 150-200 & 200-250 & 250-300 & 300-350 & 350-400 & 400-450 & 450-500 \\ \hline \text { Employees } & 5 & 3 & 5 & 6 & 8 & 7 & 5 \\ \hline \end{array}$

Ans:  

(a) Lower limit of the third class = 250

(b) Upper limit of the seventh class = 500

(c) Class boundaries of the sixth class = 400 – 450 

(d) The class mark of the fifth class = 375 

(e) The size of the second class = 50

(f) Histogram

9. Draw a histogram with frequency polygon for the following data.

$\begin{array}{|c|c|c|c|c|c|c||} \hline \text { class interval } & 25-29 & 30-34 & 35-39 & 40-44 & 45-49 & 50-54 \\ \hline \text { frequency } & 5 & 15 & 23 & 20 & 10 & 7 \\ \hline \end{array}$

Ans:  Ascertainment of lower and upper class limits: since the difference between the second and first mid-points is 25-29

Let ${\text{h}} = 1$

Then for continuous frequency distribution, we subtract $\dfrac{h}{2}$ from the lower limit and Add $\dfrac{h}{2}$ to the upper limit.

$\therefore \dfrac{h}{2} = 0.5$

$\begin{array}{||l|c|c|c|c|c|c|} \hline \text { class interval } & 24.5-29.5 & 29.5-34.5 & 34.5-39.5 & 39.5-44.5 & 44.5-49.5 & 49.5-54.5 \\ \hline \text { frequency } & 5 & 15 & 23 & 20 & 10 & 7 \\ \hline \end{array}$

10. The average score of girls in class examinations in a school is 67 and that of boys is 63. The average score for the whole class is 64.5. Find the percentage of girls and boys in the class. 

Ans:   Let the number of girls and boys be n 1 and n 2 respectively. 

$\overline {{X_1}} $ :  Average score of girls $ = 67$

$\overline {{X_2}} $ : Average score of boys $ = 63$

$X$ :  Average score of the whole class $ = 64.5$

$X = \dfrac{{{n_1}\overline {{X_1}}  + {n_2}\overline {{X_2}} }}{{{n_2} + {n_2}}}$

$ \Rightarrow 64.5 = \dfrac{{67{n_1} + 63{n_2}}}{{{n_1} + {n_2}}}$

$ \Rightarrow 64.5{{\text{n}}_{\text{1}}} + 64.5{{\text{n}}_2} = 67{{\text{n}}_1} + 63{{\text{n}}_2}$

$ \Rightarrow 2.5{{\text{n}}_1} = 1.5{{\text{n}}_2}$

$ \Rightarrow 25{{\text{n}}_1} = 15{{\text{a}}_2}$

$ \Rightarrow 5{{\text{n}}_1} = 3{{\text{n}}_2}$

Total number of students in the class $ = {n_1} + {n_2}$

$\therefore $ percentage of girls $ = \dfrac{{{n_1}}}{{{n_1} + {n_2}}} \times 100$

$ = \dfrac{{{n_1}}}{{{n_1} + \dfrac{{5{n_1}}}{3}}} \times 100$

$ = \dfrac{{3{n_1}}}{{3{n_1} + 5{n_1}}} \times 100$

$ = \dfrac{3}{8} \times 100 = 37.5$

Percentage of boys $ = \dfrac{{{n_2}}}{{{n_1} + {n_2}}} \times 100$

$ = \dfrac{{{n_2}}}{{\dfrac{{3{n_2}}}{5} + {n_2}}} \times 100$

$ = \dfrac{{5{n_2}}}{{3{n_2} + 5{n_2}}} \times 100$

11. Find the unknown entries (a, b, c, d, e, f) from the following frequency distribution of heights of 50 students in a class.

Ans:  Since the given frequency distribution is the frequency distribution of 50 students.

Therefore, $g = 50$

From the table, we have

$a = 12,\;\;b + 12 = 25,\;\;12 + b + 10 = c,\;\;12 + b + 10 + d = 43$

$12 + b + 10 + d + e = 48$ and $12 + b + 10 + d + e + g = f$

${\text{b}} + 12 = 25 \Rightarrow {\text{b}} = 13$

$12 + b + 10 = c$

$ \Rightarrow 12 + 13 + 10 = {\text{c}}$

$ \Rightarrow c = 35$

$12 + b + 10 + d - 43$

$ \Rightarrow 12 + 13 + 10 + d = 43$

$ \Rightarrow d = 8$

$12 + b + 10 + d + e = 48$

$ \Rightarrow 12 + 13 + 10 + 8 + e = 48$

$ \Rightarrow e = 5$

$12 + b + 10 + d + e + 2 = f$

$ \Rightarrow 12 + 13 + 10 + 8 + 5 + 2 = f$

$ \Rightarrow \;f = 50$

Maths Chapter 12- Statistics

The collection, arrangement, examination, interpretation, and presentation of data are defined by Statistics.

Steps in assessing the data:

Collection of data

Presentation of data (Tabular/ Graphical)

The measure of central tendency

We will address all these aspects of data briefly in this chapter.

Collection of Data

Data collection is the method by which information on targeted variables is collected and measured in a defined framework, which then helps one to answer relevant questions and analyze results.

For statistical analysis, there are several methods used to gather or collect data. Three of the methods that are most commonly used are:

Direct observation

Experimentation

Ex: In a class of 50 students a teacher has to collect the data of blood groups of all students. So this task is regarding data collection.

How this is achieved is the method of data collection.

So here the teacher can look into the documents of students to collect the blood group data or the teacher can organize a doctor to check all 50 students and collect the data.

Presentation of Data

Data presentation refers to the arrangement of data into tables, graphs or charts so that the collected measurements can draw logical and statistical conclusions.

Ex: Teacher has collected the blood groups of all 50 students and he has prepared a report to show it to the School management as follows:

Student 1- A+

Student 2- AB+

Student 3- O+

Student 4- B+

Student 5- O+

Student 6- A+

Student 7- AB+

Student 8- B-

Student 9- O+

Student 50- B-

So data represented in this way doesn’t look good and it won’t give a proper knowledge for the person who is seeing it for the first time. So the representation of data plays an important role. We can represent data using tables and graphs.

Data Representation Using Tables:

So the data represented in the table look more presentable than giving raw data.

Data Representation Using Graphs:

Graphical representation of data has three different types:

A bar chart or bar graph is a chart or graph that provides rectangular bars with categorical data with heights or lengths proportional to the values they represent. It is possible to plot the bars vertically or horizontally.

Image will be Uploaded Soon

A histogram is a graphical data display using bars of various heights. Each bar groups numbers into ranges in a histogram. Taller bars indicate that in that range, more data drop. The form and distribution of continuous sample data are shown in a histogram.

A pie chart is a circular statistical graph which, to illustrate numerical proportions, is divided into slices. In a pie map, each slice's arc length is equal to the sum that it represents.

The Measure of Central Tendency

By using frequency distribution tables, bar graphs, histograms and frequency polygons, we depicted the data in different types. Now, whether we still need to analyze all the data in order to make sense of it, or whether we can define some essential features of it by considering only some data members, the question arises. By using a measure of central tendency, this is possible.

The measure of central tendency includes a summary measure seeking to characterize a whole set of single-value data reflecting the middle or centre of its distribution.

The measure of central tendency helps us to locate the centre of a data set, or the average. The Mean, Median, and Mode are the 3 most common measures of central tendency.

The sum of all values divided by the total number of values is the arithmetical mean of a data set. It is the most widely used central tendency metric since the equation uses all values for calculation.

Formula to calculate the Mean is 

Mean (x̄) = Sum of the given data/ total number of data

Ex: There are 5 students whose marks are as follows. Calculate the Mean marks.

To calculate the mean first we have to find the sum of the marks of 5 students.

Sum of marks = 80+60+75+95+35= 350

Number of students = 5

Mean = Sum of marks / Number of students

Mean = 350/5 = 70.

The Mean of the marks is 70. That is, the average marks obtained is 70.

When the data is sorted ascending or descending, the median of a data set is the value that is exactly in the centre.

Ex: Calculate the median for the given set of data.

So here there is an odd number of students i.e 5. So the median will be the marks obtained by the 3rd student who is the centre of the data.

Therefore the median value is 75.

Mode: 

The most frequently occurring value in the data set is the mode. There can be no mode, one mode, or more than one mode. 

To find mode sort the data set numerically or categorically to find the mode, and choose the answer that occurs most often.

Ex: Find the mode for the following data set.

Here 40 marks have been scored by 2nd and 5th students. So this mark is repetitive in the data. Therefore the mode of the following data set is 40 as it occurs more often.

When to Use Mean, Median and Mode?

In conjunction with each other, the 3 main measures of central tendency are best used because they have complementary strengths and weaknesses. But sometimes only 1 or 2 of them are applicable to our data set, depending on the level of measurement of the variable.

The mean can only be used on measurement interval and ratio levels since it needs equal spacing in the scale between adjacent values or ratings.

The median can only be used on data that can be ordered, that is, from measurement levels of ordinal, interval and ratio.

The mode can be used for any measurement level, but for nominal and ordinal levels, it is most appropriate.

For more information on Class 9 Maths Chapter 12 Important Questions of Statistics students can go through the free NCERT notes and Solutions provided by Vedantu to get deep knowledge on the topic and to score good marks in their exams.

Practice Questions from CBSE Class 9 Maths Chapter 12 - Statistics

1. The mean of 20 observations is 17. If in the observations, observation 40 is replaced by 12, then find the new mean.

2. If the mean of five observations x, x + 2, x + 4, x + 6, and x + 8 is 11, then write the value of x.

3. Write the class mark of an interval 90 – 120.

4. The mean of 8 observations is 40. If 5 is added to each observation, then what will be the new mean?

5. Find the median of the values 37, 31, 42, 43, 46, 25, 39, 45, and 32.

6. The median of the data 26, 56, 32, 33, 60, 17, 34, 29, and 45 is 33. If 26 is replaced by 62, then find the new median.

7. The class marks of a frequency distribution are 104, 114, 124, 134, 144, 154, and 164. Find the class size and class intervals.

8. The mean weight per student in a group of 7 students is 55 kg. The individual weights of 6 of them in kg are 52, 54, 55, 53, 56, and 54. Find the weight of the seventh student.

9. The questions solved by a student during a week are as follows: Find the mean.

Key Features of Important Questions CBSE Class 9 Maths Chapter 12 - Statistics

Exam-Oriented Content: Class 9 Maths Chapter 12 - Statistics includes crucial questions tailored for exams to ensure comprehensive preparation.

Detailed Solutions: Thorough and step-by-step explanations for all questions, aiding in a deeper understanding of the concepts.

Expert-Crafted Solutions: Solutions crafted by experienced Maths subject experts, aligning with the curriculum for easy comprehension.

Foundation Building: Important questions contribute to building a strong foundation crucial for success in board and competitive exams.

Free and Accessible: Solutions are freely available, downloadable in a convenient PDF format for easy access and offline studying.

Important Related Links for CBSE Class 9 

Important Questions for CBSE Class 9 Maths Chapter 12 Statistics are a very important study material for students preparing for the Class 9 final Examination. Here we have given important questions with solutions from very important topics that are covered by NCERT Class 9 Maths Syllabus . Students will also get an idea about the type of questions and method to answer the final examination.

FAQs on Important Questions for CBSE Class 9 Maths Chapter 12 - Statistics

1. How many chapters are covered in Class 9th Maths Important Questions apart from Statistics?

Overall, 15 chapters are covered in Important Questions for Class 9 Maths. They provide a thorough understanding of how the chapters agree with the overall subject matter as prescribed in the course.

2. How can Class 9 students practise Maths?

Students of Class 9 can practise Maths from the NCERT Solutions, Revision Notes, and Important Questions available on Vedantu. Students can also practise with extra questions given on Vedantu to understand the concepts and score good marks in Class 9 Maths. All concepts and solutions are explained in detail by expert Maths subject experts.

3. How could I learn CBSE Class 9 Maths Chapter 12 - Statistics in an efficient and fast way?

Students can learn CBSE Class 9 Maths Chapter 12 - Statistics by practising all questions from NCERT solutions provided by Vedantu. Students can use revision notes to  revise chapters to understand the concepts. Also, solve important questions given here and get high marks in exams

4. What are the important concepts covered in CBSE Class 9 Maths Chapter 12 - Statistics?

Important concepts covered in CBSE Class 9 Maths Chapter 12 - Statistics are as follows:

Collection of data 

Measure of central tendency

5. Are these important questions from CBSE Class 9 Maths Chapter 12 - Statistics free to download?

Yes, CBSE Class 9 Maths Chapter 12 - Statistics are free to download. Students can access Free PDF with just a click.

6. The mean weight of a class of 34 students is 46.5 kg. If the weight of the new boy is included, the mean is rises by 500 g. Find the weight of the new boy.

The mean weight of 34 students = 46.5

Sum of the weight of 34 students = (46.5 * 34) = 1581

Change or increase in the mean weight when the weight of a new boy is added = 0.5

So, the new mean = (46.5 +0.5) = 47

So, let the weight of the new boy be y.

So, (sum of weight of 34 students + weight of new boy) / 35 = 47

(1581+ y)/ 35 = 47

1581 + y = 1645

y = 1645 – 1581 = 64

7. Mean of 20 observations is 17. If in the observations, observation 40 is replaced by 12, find the new mean.

Since mean of 20 observations is 17 ∴ Sum of the 20 observations = 17 × 20 = 340 New sum of 20 observations = 340 – 40 + 12 = 312 New mean = 312/20 = 15.6

8. The mean weight of 60 students of a class is 52.75 kg. If mean weight of 25 students of this class is 51 kg, find the mean weight of remaining 35 students of the class.

Total weight of 60 students = 60 × 52.75 kg = 3165 kg Total weight of 25 students = 25 × 51 kg = 1275 kg ∴ Total weight of 35 students = (3165 – 1275) kg = 1890 kg ∴ Mean weight of 35 students = 189035 = 54 kg

9. The points scored by a basketball team in a series of matches are as follows: 17, 7, 10, 25, 5, 10, 18, 10 and 24. Find the range.

17, 7, 10, 25, 5, 10, 18, 10 and 24. Find the range.

Here, maximum points = 25 and Minimum points = 5 Range = Maximum value – Minimum value = 25 – 5 = 20

10. How students can score good marks in statistics class 9.

Students can score good marks in statistics class 9 by revising each exercise 2-3 times. Also, they need to solve sample papers to improve their time management and accuracy. Students can also solve sample papers on Vendantu site.

CBSE Class 9 Maths Important Questions

Cbse study materials.

(Education-Your Door To The Future)

CBSE Class 9 Maths Most Important Case Study Based Questions With Solution

Cbse class 9 mathematics case study questions.

In this post I have provided CBSE Class 9 Maths Case Study Based Questions With Solution. These questions are very important for those students who are preparing for their final class 9 maths exam.

All these questions provided in this article are with solution which will help students for solving the problems. Dear students need to practice all these questions carefully with the help of given solutions.

As you know CBSE Class 9 Maths exam will have a set of cased study based questions in the form of MCQs. CBSE Class 9 Maths Question Bank given in this article can be very helpful in understanding the new format of questions for new session.

All Of You Can Also Read

Case studies in class 9 mathematics.

The Central Board of Secondary Education (CBSE) has included case study based questions in the Class 9 Mathematics paper in current session. According to new pattern CBSE Class 9 Mathematics students will have to solve case based questions. This is a departure from the usual theoretical conceptual questions that are asked in Class 9 Maths exam in this year.

Each question provided in this post has five sub-questions, each followed by four options and one correct answer. All CBSE Class 9th Maths Students can easily download these questions in PDF form with the help of given download Links and refer for exam preparation.

There is many more free study materials are available at Maths And Physics With Pandey Sir website. For many more books and free study material all of you can visit at this website.

Given Below Are CBSE Class 9th Maths Case Based Questions With Their Respective Download Links.

• NCERT Solutions
• NCERT Class 9
• NCERT 9 Maths
• Chapter 12: Herons Formula
• Exercise 12.1

NCERT Solutions for Class 9 Maths Chapter 12 - Heron's Formula Exercise 12.1

* According to the CBSE Syllabus 2023-24, this chapter has been renumbered as Chapter 10.

NCERT Solutions for Class 9 Maths Chapter 12 – Heron’s Formula Exercise 12.1 helps you understand Heron’s Formula with ease. From an academic perspective, this fundamental concept finds significance in a myriad of areas. Therefore, it is necessary to have a clear grasp of the concept. These solutions are designed by highly knowledgeable teachers with countless years of experience. In other words, NCERT Solutions is one of the best guides for your study needs. Relevant topics are presented in an easy-to-understand format. Moreover, we have barred the use of complex jargon. Furthermore, its content is updated regularly as per the prescribed CBSE syllabus.

Download PDF of NCERT Solutions for Class 9 Maths Chapter 12 – Heron’s Formula Exercise 12.1

carouselExampleControls111

Access other exercise solutions of Class 9 Maths Chapter 12 – Heron’s Formula

Exercise 12.2 Solutions – 9 Questions

Access Answers of Maths NCERT Class 9 Chapter 12 – Heron’s Formula Exercise 12.1

1. A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?

Side of the signal board = a

Perimeter of the signal board = 3a = 180 cm

∴ a = 60 cm

Semi perimeter of the signal board (s) = 3a/2

By using Heron’s formula,

Area of the triangular signal board will be =

2. The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see Fig. 12.9). The advertisements yield an earning of ₹5000 per m 2 per year. A company hired one of its walls for 3 months. How much rent did it pay?

The sides of the triangle ABC are 122 m, 22 m and 120 m respectively.

Now, the perimeter will be (122+22+120) = 264 m

Also, the semi perimeter (s) = 264/2 = 132 m

Using Heron’s formula,

Area of the triangle =

We know that the rent of advertising per year = ₹ 5000 per m 2

∴ The rent of one wall for 3 months = Rs. (1320×5000×3)/12 = Rs. 1650000

3. There is a slide in a park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see Fig. 12.10 ). If the sides of the wall are 15 m, 11 m and 6 m, find the area painted in colour.

It is given that the sides of the wall as 15 m, 11 m and 6 m.

So, the semi perimeter of triangular wall (s) = (15+11+6)/2 m = 16 m

Area of the message =

= √[16(16-15)(16-11) (16-6)] m 2

= √[16×1×5×10] m 2 = √800 m 2

4. Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42cm.

Assume the third side of the triangle to be “x”.

Now, the three sides of the triangle are 18 cm, 10 cm, and “x” cm

It is given that the perimeter of the triangle = 42cm

So, x = 42-(18+10) cm = 14 cm

∴ The semi perimeter of triangle = 42/2 = 21 cm

Area of the triangle,

= √[21(21-18)(21-10)(21-14)] cm 2

= √[21×3×11×7] m 2

= 21√11 cm 2

5. Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540cm. Find its area.

The ratio of the sides of the triangle are given as 12 : 17 : 25

Now, let the common ratio between the sides of the triangle be “x”

∴ The sides are 12x, 17x and 25x

It is also given that the perimeter of the triangle = 540 cm

12x+17x+25x = 540 cm

54x = 540cm

Now, the sides of triangle are 120 cm, 170 cm, 250 cm.

So, the semi perimeter of the triangle (s) = 540/2 = 270 cm

Area of the triangle

= 9000 cm 2

6. An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.

First, let the third side be x.

It is given that the length of the equal sides is 12 cm and its perimeter is 30 cm.

So, 30 = 12+12+x

∴ The length of the third side = 6 cm

Thus, the semi perimeter of the isosceles triangle (s) = 30/2 cm = 15 cm

= √[15(15-12)(15-12)(15-6)] cm 2

= √[15×3×3×9] cm 2

= 9√15 cm 2

Heron’s formula is used to find the area of a triangle, provided the length of the 3 sides is given. Apart from the formula, Heron contributed in many other ways, and the most notable was the invention of the very first steam engine. It was called the Aeolipile, and technically, it didn’t resemble an engine. However, no practical applications could be identified, and instead, it was used as a toy and a novelty for the ancient Greeks. Explore more about Heron’s Formula, learn how to solve related problems and more only on NCERT Solutions For Class 9 Maths .

Key Features of NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula Exercise 12.1

• Structured content
• Important formulas are highlighted
• Simple language with jargon-free explanations
• Solutions provided by qualified teachers
• Updated questions with solutions
• A thorough breakdown of tough questions

Explore: NCERT Solutions Class 9

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

All teachers are best

Awesome teachers 😍

Awesome, this website helped me!

Awesome, this is the best website ever i saw in my life. It helps me alot. I always came to this website for any solution or any dout BYJU’S always help me

Awesome , this is the best website ever i saw in my life. It always help me

Awesome, it is the best website

It is the best website

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.