hypothesis testing chi square test of independence

JMP | Statistical Discovery.™ From SAS.

Statistics Knowledge Portal

A free online introduction to statistics

Chi-Square Test of Independence

What is the chi-square test of independence.

The Chi-square test of independence is a statistical hypothesis test used to determine whether two categorical or nominal variables are likely to be related or not.

When can I use the test?

You can use the test when you have counts of values for two categorical variables.

Can I use the test if I have frequency counts in a table?

Yes. If you have only a table of values that shows frequency counts, you can use the test.

Using the Chi-square test of independence

See how to perform a chi-square test of independence using statistical software.

• Download JMP to follow along using the sample data included with the software.
• To see more JMP tutorials, visit the JMP Learning Library .

The Chi-square test of independence checks whether two variables are likely to be related or not. We have counts for two categorical or nominal variables. We also have an idea that the two variables are not related. The test gives us a way to decide if our idea is plausible or not.

The sections below discuss what we need for the test, how to do the test, understanding results, statistical details and understanding p-values.

What do we need?

For the Chi-square test of independence, we need two variables. Our idea is that the variables are not related. Here are a couple of examples:

• We have a list of movie genres; this is our first variable. Our second variable is whether or not the patrons of those genres bought snacks at the theater. Our idea (or, in statistical terms, our null hypothesis) is that the type of movie and whether or not people bought snacks are unrelated. The owner of the movie theater wants to estimate how many snacks to buy. If movie type and snack purchases are unrelated, estimating will be simpler than if the movie types impact snack sales.
• A veterinary clinic has a list of dog breeds they see as patients. The second variable is whether owners feed dry food, canned food or a mixture. Our idea is that the dog breed and types of food are unrelated. If this is true, then the clinic can order food based only on the total number of dogs, without consideration for the breeds.

For a valid test, we need:

• Data values that are a simple random sample from the population of interest.
• Two categorical or nominal variables. Don't use the independence test with continous variables that define the category combinations. However, the counts for the combinations of the two categorical variables will be continuous.
• For each combination of the levels of the two variables, we need at least five expected values. When we have fewer than five for any one combination, the test results are not reliable.

Chi-square test of independence example

Let’s take a closer look at the movie snacks example. Suppose we collect data for 600 people at our theater. For each person, we know the type of movie they saw and whether or not they bought snacks.

Let’s start by answering: Is the Chi-square test of independence an appropriate method to evaluate the relationship between movie type and snack purchases?

• We have a simple random sample of 600 people who saw a movie at our theater. We meet this requirement.
• Our variables are the movie type and whether or not snacks were purchased. Both variables are categorical. We meet this requirement.
• The last requirement is for more than five expected values for each combination of the two variables. To confirm this, we need to know the total counts for each type of movie and the total counts for whether snacks were bought or not. For now, we assume we meet this requirement and will check it later. 

It appears we have indeed selected a valid method. (We still need to check that more than five values are expected for each combination.)

Here is our data summarized in a contingency table:

Table 1: Contingency table for movie snacks data

Before we go any further, let’s check the assumption of five expected values in each category. The data has more than five counts in each combination of Movie Type and Snacks. But what are the expected counts if movie type and snack purchases are independent?

Finding expected counts

To find expected counts for each Movie-Snack combination, we first need the row and column totals, which are shown below:

Table 2: Contingency table for movie snacks data with row and column totals

The expected counts for each Movie-Snack combination are based on the row and column totals. We multiply the row total by the column total and then divide by the grand total. This gives us the expected count for each cell in the table. For example, for the Action-Snacks cell, we have:

$ \frac{125\times310}{600} = \frac{38,750}{600} = 65 $

We rounded the answer to the nearest whole number. If there is not a relationship between movie type and snack purchasing we would expect 65 people to have watched an action film with snacks.

Here are the actual and expected counts for each Movie-Snack combination. In each cell of Table 3 below, the expected count appears in bold beneath the actual count. The expected counts are rounded to the nearest whole number.

Table 3: Contingency table for movie snacks data showing actual count vs. expected count

When using  software, these calculated values will be labeled as “expected values,” “expected cell counts” or some similar term.

All of the expected counts for our data are larger than five, so we meet the requirement for applying the independence test.

Before calculating the test statistic, let’s look at the contingency  table again. The expected counts use the row and column totals. If we look at each of the cells, we can see that some expected counts are close to the actual counts but most are not. If there is no relationship between the movie type and snack purchases, the actual and expected counts will be similar. If there is a relationship, the actual and expected counts will be different.

A common mistake with expected counts is to simply divide the grand total by the number of cells. For our movie data, this is 600 / 8 = 75. This is not correct. We know the row totals and column totals. These are fixed and cannot change for our data. The expected values are based on the row and column totals, not just on the grand total.

Performing the test

The basic idea in calculating the test statistic is to compare actual and expected values, given the row and column totals that we have in the data. First, we calculate the difference from actual and expected for each Movie-Snacks combination. Next, we square that difference. Squaring gives the same importance to combinations with fewer actual values than expected and combinations with more actual values than expected. Next, we divide by the expected value for the combination. We add up these values for each Movie-Snacks combination. This gives us our test statistic.

This is much easier to follow using the data from our example. Table 4 below shows the calculations for each Movie-Snacks combination carried out to two decimal places.  

Table 4: Preparing to calculate our test statistic

Lastly, to get our test statistic, we add the numbers in the final row for each cell:

$ 3.29 + 3.52 + 5.81 + 6.21 + 12.65 + 13.52 + 9.68 + 10.35 = 65.03 $

To make our decision, we compare the test statistic to a value from the Chi-square distribution . This activity involves five steps:

• We decide on the risk we are willing to take of concluding that the two variables are not independent when in fact they are. For the movie data, we had decided prior to our data collection that we are willing to take a 5% risk of saying that the two variables – Movie Type and Snack Purchase – are not independent when they really are independent. In statistics-speak, we set the significance level, α, to 0.05.
• We calculate a test statistic. As shown above, our test statistic is 65.03.
• We find the critical value from the Chi-square distribution based on our degrees of freedom and our significance level. This is the value we expect if the two variables are independent.
• The degrees of freedom depend on how many rows and how many columns we have. The degrees of freedom (df) are calculated as: $ \text{df} = (r-1)\times(c-1) $ In the formula, r is the number of rows, and c is the number of columns in our contingency table. From our example, with Movie Type as the rows and Snack Purchase as the columns, we have: $ \text{df} = (4-1)\times(2-1) = 3\times1 = 3 $ The Chi-square value with α = 0.05 and three degrees of freedom is 7.815.
• We compare the value of our test statistic (65.03) to the Chi-square value. Since 65.03 > 7.815, we reject the idea that movie type and snack purchases are independent.

We conclude that there is some relationship between movie type and snack purchases. The owner of the movie theater cannot estimate how many snacks to buy regardless of the type of movies being shown. Instead, the owner must think about the type of movies being shown when estimating snack purchases.

It's important to note that we cannot conclude that the type of movie causes a snack purchase. The independence test tells us only whether there is a relationship or not; it does not tell us that one variable causes the other.

Understanding results

Let’s use graphs to understand the test and the results.

The side-by-side chart below shows the actual counts in blue, and the expected counts in orange. The counts appear at the top of the bars. The yellow box shows the movie type and snack purchase totals. These totals are needed to find the expected counts. 

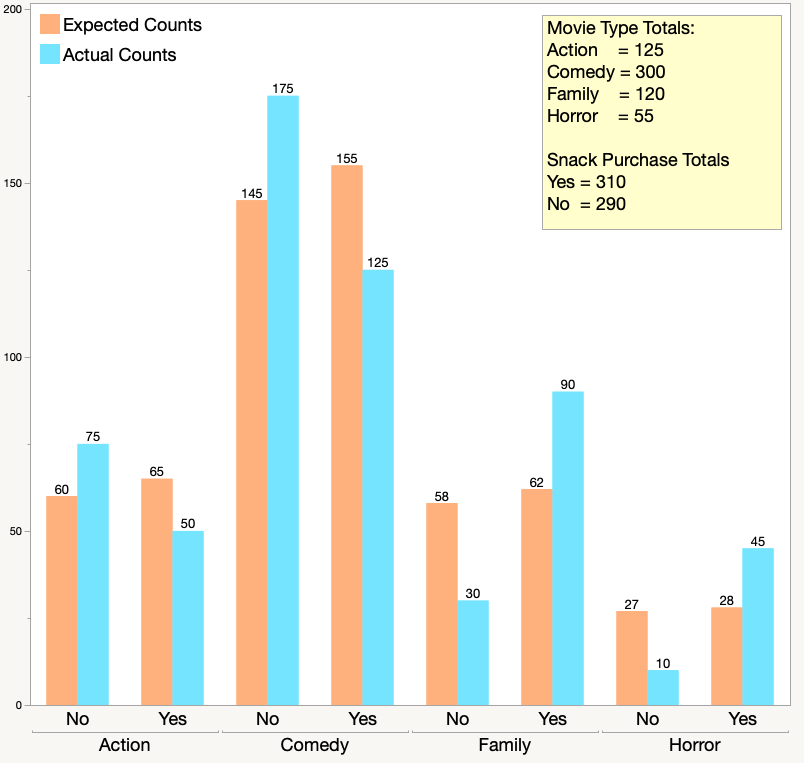
Compare the expected and actual counts for the Horror movies. You can see that more people than expected bought snacks and fewer people than expected chose not to buy snacks.

If you look across all four of the movie types and whether or not people bought snacks, you can see that there is a fairly large difference between actual and expected counts for most combinations. The independence test checks to see if the actual data is “close enough” to the expected counts that would occur if the two variables are independent. Even without a statistical test, most people would say that the two variables are not independent. The statistical test provides a common way to make the decision, so that everyone makes the same decision on the data.

The chart below shows another possible set of data. This set has the exact same row and column totals for movie type and snack purchase, but the yes/no splits in the snack purchase data are different. 

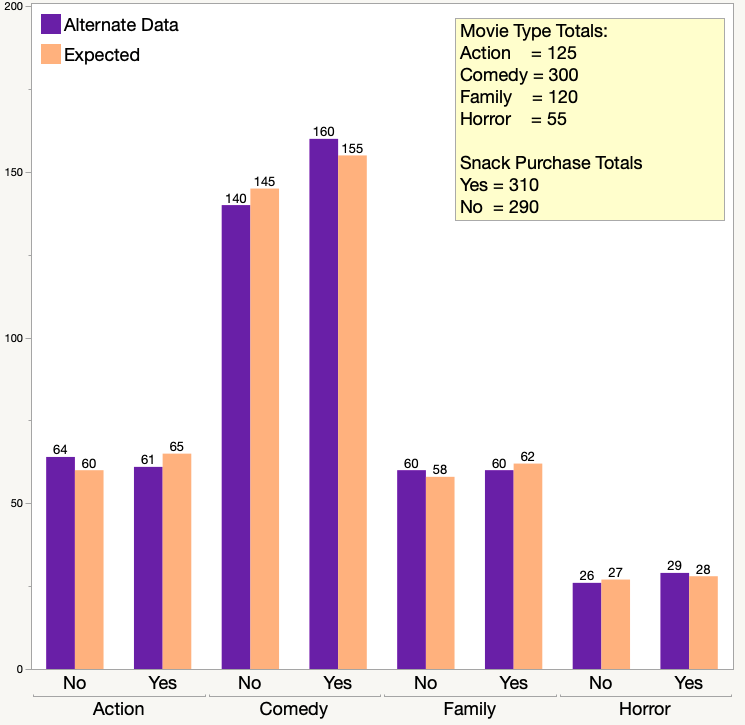
The purple bars show the actual counts in this data. The orange bars show the expected counts, which are the same as in our original data set. The expected counts are the same because the row totals and column totals are the same. Looking at the graph above, most people would think that the type of movie and snack purchases are independent. If you perform the Chi-square test of independence using this new data, the test statistic is 0.903. The Chi-square value is still 7.815 because the degrees of freedom are still three. You would fail to reject the idea of independence because 0.903 < 7.815. The owner of the movie theater can estimate how many snacks to buy regardless of the type of movies being shown. 

Statistical details

Let’s look at the movie-snack data and the Chi-square test of independence using statistical terms.

Our null hypothesis is that the type of movie and snack purchases are independent. The null hypothesis is written as:

$ H_0: \text{Movie Type and Snack purchases are independent} $

The alternative hypothesis is the opposite.

$ H_a: \text{Movie Type and Snack purchases are not independent} $

Before we calculate the test statistic, we find the expected counts. This is written as:

$ Σ_{ij} = \frac{R_i\times{C_j}}{N} $

The formula is for an i x j contingency table. That is a table with i rows and j columns. For example, E 11 is the expected count for the cell in the first row and first column. The formula shows R i as the row total for the i th row, and C j as the column total for the j th row. The overall sample size is N .  

We calculate the test statistic using the formula below:

$ Σ^n_{i,j=1} = \frac{(O_{ij}-E_{ij})^2}{E_{ij}} $

In the formula above, we have n combinations of rows and columns. The Σ symbol means to add up the calculations for each combination. (We performed these same steps in the Movie-Snack example, beginning in Table 4.) The formula shows O ij as the Observed count for the ij -th combination and E i j   as the Expected count for the combination. For the Movie-Snack example, we had four rows and two columns, so we had eight combinations.

We then compare the test statistic to the critical Chi-square value corresponding to our chosen alpha value and the degrees of freedom for our data. Using the Movie-Snack data as an example, we had set α = 0.05 and had three degrees of freedom. For the Movie-Snack data, the Chi-square value is written as:

$ χ_{0.05,3}^2 $

There are two possible results from our comparison:

• The test statistic is lower than the Chi-square value. You fail to reject the hypothesis of independence. In the movie-snack example, the theater owner can go ahead with the assumption that the type of movie a person sees has no relationship with whether or not they buy snacks.
• The test statistic is higher than the Chi-square value. You reject the hypothesis of independence. In the movie-snack example, the theater owner cannot assume that there is no relationship between the type of movie a person sees and whether or not they buy snacks.

Understanding p-values

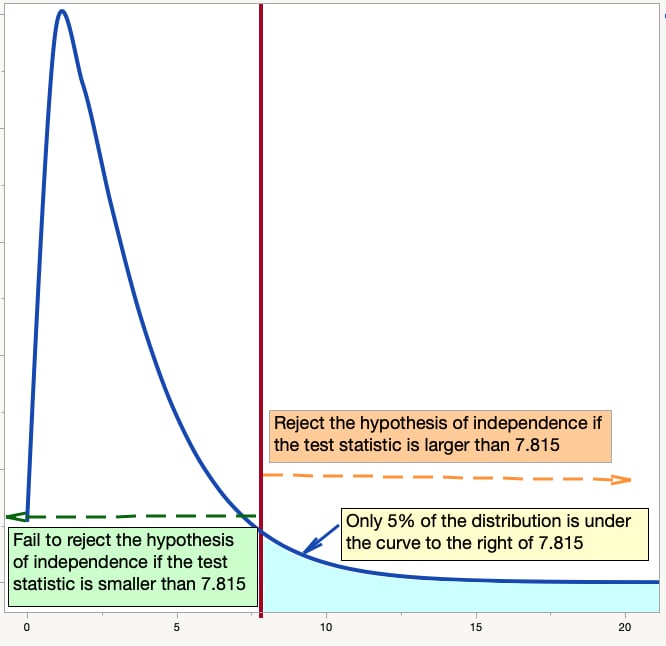
Let’s use a graph of the Chi-square distribution to better understand the p-values. You are checking to see if your test statistic is a more extreme value in the distribution than the critical value. The graph below shows a Chi-square distribution with three degrees of freedom. It shows how the value of 7.815 “cuts off” 95% of the data. Only 5% of the data from a Chi-square distribution with three degrees of freedom is greater than 7.815.

The next distribution graph shows our results. You can see how far out “in the tail” our test statistic is. In fact, with this scale, it looks like the distribution curve is at zero at the point at which it intersects with our test statistic. It isn’t, but it is very, very close to zero. We conclude that it is very unlikely for this situation to happen by chance. The results that we collected from our movie goers would be extremely unlikely if there were truly no relationship between types of movies and snack purchases.

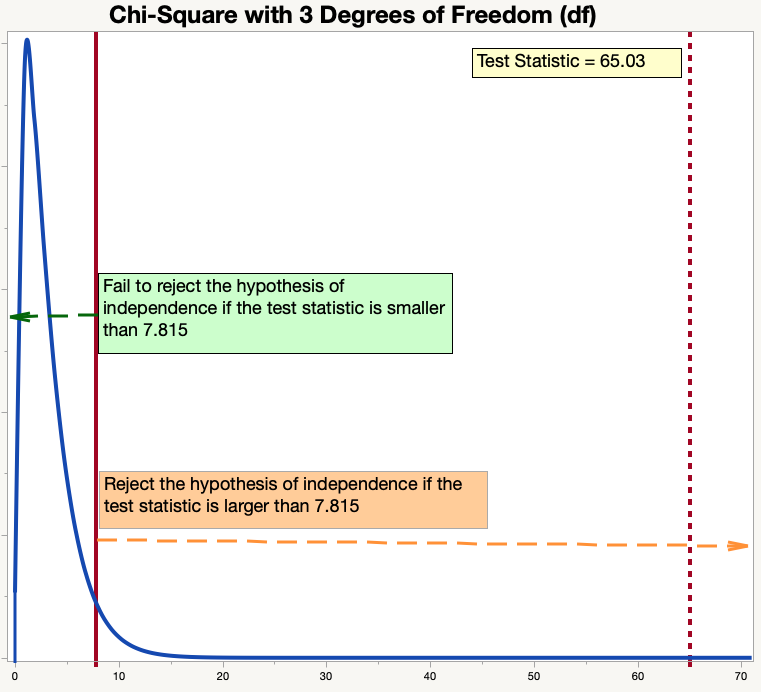
Statistical software shows the p-value for a test. This is the likelihood of another sample of the same size resulting in a test statistic more extreme than the test statistic from our current sample, assuming that the null hypothesis is true. It’s difficult to calculate this by hand. For the distributions shown above, if the test statistic is exactly 7.815, then the p - value will be p=0.05. With the test statistic of 65.03, the p - value is very, very small. In this example, most statistical software will report the p - value as “p < 0.0001.” This means that the likelihood of finding a more extreme value for the test statistic using another random sample (and assuming that the null hypothesis is correct) is less than one chance in 10,000.

Hypothesis Testing - Chi Squared Test

Lisa Sullivan, PhD

Professor of Biostatistics

Boston University School of Public Health

Introduction

This module will continue the discussion of hypothesis testing, where a specific statement or hypothesis is generated about a population parameter, and sample statistics are used to assess the likelihood that the hypothesis is true. The hypothesis is based on available information and the investigator's belief about the population parameters. The specific tests considered here are called chi-square tests and are appropriate when the outcome is discrete (dichotomous, ordinal or categorical). For example, in some clinical trials the outcome is a classification such as hypertensive, pre-hypertensive or normotensive. We could use the same classification in an observational study such as the Framingham Heart Study to compare men and women in terms of their blood pressure status - again using the classification of hypertensive, pre-hypertensive or normotensive status.  

The technique to analyze a discrete outcome uses what is called a chi-square test. Specifically, the test statistic follows a chi-square probability distribution. We will consider chi-square tests here with one, two and more than two independent comparison groups.

Learning Objectives

After completing this module, the student will be able to:

• Perform chi-square tests by hand
• Appropriately interpret results of chi-square tests
• Identify the appropriate hypothesis testing procedure based on type of outcome variable and number of samples

Tests with One Sample, Discrete Outcome

Here we consider hypothesis testing with a discrete outcome variable in a single population. Discrete variables are variables that take on more than two distinct responses or categories and the responses can be ordered or unordered (i.e., the outcome can be ordinal or categorical). The procedure we describe here can be used for dichotomous (exactly 2 response options), ordinal or categorical discrete outcomes and the objective is to compare the distribution of responses, or the proportions of participants in each response category, to a known distribution. The known distribution is derived from another study or report and it is again important in setting up the hypotheses that the comparator distribution specified in the null hypothesis is a fair comparison. The comparator is sometimes called an external or a historical control.   

In one sample tests for a discrete outcome, we set up our hypotheses against an appropriate comparator. We select a sample and compute descriptive statistics on the sample data. Specifically, we compute the sample size (n) and the proportions of participants in each response

Test Statistic for Testing H 0 : p 1 = p 10 , p 2 = p 20 , ..., p k = p k0

We find the critical value in a table of probabilities for the chi-square distribution with degrees of freedom (df) = k-1. In the test statistic, O = observed frequency and E=expected frequency in each of the response categories. The observed frequencies are those observed in the sample and the expected frequencies are computed as described below. χ 2 (chi-square) is another probability distribution and ranges from 0 to ∞. The test above statistic formula above is appropriate for large samples, defined as expected frequencies of at least 5 in each of the response categories.  

When we conduct a χ 2 test, we compare the observed frequencies in each response category to the frequencies we would expect if the null hypothesis were true. These expected frequencies are determined by allocating the sample to the response categories according to the distribution specified in H 0 . This is done by multiplying the observed sample size (n) by the proportions specified in the null hypothesis (p 10 , p 20 , ..., p k0 ). To ensure that the sample size is appropriate for the use of the test statistic above, we need to ensure that the following: min(np 10 , n p 20 , ..., n p k0 ) > 5.  

The test of hypothesis with a discrete outcome measured in a single sample, where the goal is to assess whether the distribution of responses follows a known distribution, is called the χ 2 goodness-of-fit test. As the name indicates, the idea is to assess whether the pattern or distribution of responses in the sample "fits" a specified population (external or historical) distribution. In the next example we illustrate the test. As we work through the example, we provide additional details related to the use of this new test statistic.  

A University conducted a survey of its recent graduates to collect demographic and health information for future planning purposes as well as to assess students' satisfaction with their undergraduate experiences. The survey revealed that a substantial proportion of students were not engaging in regular exercise, many felt their nutrition was poor and a substantial number were smoking. In response to a question on regular exercise, 60% of all graduates reported getting no regular exercise, 25% reported exercising sporadically and 15% reported exercising regularly as undergraduates. The next year the University launched a health promotion campaign on campus in an attempt to increase health behaviors among undergraduates. The program included modules on exercise, nutrition and smoking cessation. To evaluate the impact of the program, the University again surveyed graduates and asked the same questions. The survey was completed by 470 graduates and the following data were collected on the exercise question:

Based on the data, is there evidence of a shift in the distribution of responses to the exercise question following the implementation of the health promotion campaign on campus? Run the test at a 5% level of significance.

In this example, we have one sample and a discrete (ordinal) outcome variable (with three response options). We specifically want to compare the distribution of responses in the sample to the distribution reported the previous year (i.e., 60%, 25%, 15% reporting no, sporadic and regular exercise, respectively). We now run the test using the five-step approach.  

• Step 1. Set up hypotheses and determine level of significance.

The null hypothesis again represents the "no change" or "no difference" situation. If the health promotion campaign has no impact then we expect the distribution of responses to the exercise question to be the same as that measured prior to the implementation of the program.

H 0 : p 1 =0.60, p 2 =0.25, p 3 =0.15,  or equivalently H 0 : Distribution of responses is 0.60, 0.25, 0.15  

H 1 :   H 0 is false.          α =0.05

Notice that the research hypothesis is written in words rather than in symbols. The research hypothesis as stated captures any difference in the distribution of responses from that specified in the null hypothesis. We do not specify a specific alternative distribution, instead we are testing whether the sample data "fit" the distribution in H 0 or not. With the χ 2 goodness-of-fit test there is no upper or lower tailed version of the test.

• Step 2. Select the appropriate test statistic.  

The test statistic is:

We must first assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ..., n p k ) > 5. The sample size here is n=470 and the proportions specified in the null hypothesis are 0.60, 0.25 and 0.15. Thus, min( 470(0.65), 470(0.25), 470(0.15))=min(282, 117.5, 70.5)=70.5. The sample size is more than adequate so the formula can be used.

• Step 3. Set up decision rule.  

The decision rule for the χ 2 test depends on the level of significance and the degrees of freedom, defined as degrees of freedom (df) = k-1 (where k is the number of response categories). If the null hypothesis is true, the observed and expected frequencies will be close in value and the χ 2 statistic will be close to zero. If the null hypothesis is false, then the χ 2 statistic will be large. Critical values can be found in a table of probabilities for the χ 2 distribution. Here we have df=k-1=3-1=2 and a 5% level of significance. The appropriate critical value is 5.99, and the decision rule is as follows: Reject H 0 if χ 2 > 5.99.

• Step 4. Compute the test statistic.  

We now compute the expected frequencies using the sample size and the proportions specified in the null hypothesis. We then substitute the sample data (observed frequencies) and the expected frequencies into the formula for the test statistic identified in Step 2. The computations can be organized as follows.

Notice that the expected frequencies are taken to one decimal place and that the sum of the observed frequencies is equal to the sum of the expected frequencies. The test statistic is computed as follows:

• Step 5. Conclusion.  

We reject H 0 because 8.46 > 5.99. We have statistically significant evidence at α=0.05 to show that H 0 is false, or that the distribution of responses is not 0.60, 0.25, 0.15.  The p-value is p < 0.005.  

In the χ 2 goodness-of-fit test, we conclude that either the distribution specified in H 0 is false (when we reject H 0 ) or that we do not have sufficient evidence to show that the distribution specified in H 0 is false (when we fail to reject H 0 ). Here, we reject H 0 and concluded that the distribution of responses to the exercise question following the implementation of the health promotion campaign was not the same as the distribution prior. The test itself does not provide details of how the distribution has shifted. A comparison of the observed and expected frequencies will provide some insight into the shift (when the null hypothesis is rejected). Does it appear that the health promotion campaign was effective?  

Consider the following: 

If the null hypothesis were true (i.e., no change from the prior year) we would have expected more students to fall in the "No Regular Exercise" category and fewer in the "Regular Exercise" categories. In the sample, 255/470 = 54% reported no regular exercise and 90/470=19% reported regular exercise. Thus, there is a shift toward more regular exercise following the implementation of the health promotion campaign. There is evidence of a statistical difference, is this a meaningful difference? Is there room for improvement?

The National Center for Health Statistics (NCHS) provided data on the distribution of weight (in categories) among Americans in 2002. The distribution was based on specific values of body mass index (BMI) computed as weight in kilograms over height in meters squared. Underweight was defined as BMI< 18.5, Normal weight as BMI between 18.5 and 24.9, overweight as BMI between 25 and 29.9 and obese as BMI of 30 or greater. Americans in 2002 were distributed as follows: 2% Underweight, 39% Normal Weight, 36% Overweight, and 23% Obese. Suppose we want to assess whether the distribution of BMI is different in the Framingham Offspring sample. Using data from the n=3,326 participants who attended the seventh examination of the Offspring in the Framingham Heart Study we created the BMI categories as defined and observed the following:

• Step 1.  Set up hypotheses and determine level of significance.

H 0 : p 1 =0.02, p 2 =0.39, p 3 =0.36, p 4 =0.23     or equivalently

H 0 : Distribution of responses is 0.02, 0.39, 0.36, 0.23

H 1 :   H 0 is false.        α=0.05

The formula for the test statistic is:

We must assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ..., n p k ) > 5. The sample size here is n=3,326 and the proportions specified in the null hypothesis are 0.02, 0.39, 0.36 and 0.23. Thus, min( 3326(0.02), 3326(0.39), 3326(0.36), 3326(0.23))=min(66.5, 1297.1, 1197.4, 765.0)=66.5. The sample size is more than adequate, so the formula can be used.

Here we have df=k-1=4-1=3 and a 5% level of significance. The appropriate critical value is 7.81 and the decision rule is as follows: Reject H 0 if χ 2 > 7.81.

We now compute the expected frequencies using the sample size and the proportions specified in the null hypothesis. We then substitute the sample data (observed frequencies) into the formula for the test statistic identified in Step 2. We organize the computations in the following table.

The test statistic is computed as follows:

We reject H 0 because 233.53 > 7.81. We have statistically significant evidence at α=0.05 to show that H 0 is false or that the distribution of BMI in Framingham is different from the national data reported in 2002, p < 0.005.  

Again, the χ 2   goodness-of-fit test allows us to assess whether the distribution of responses "fits" a specified distribution. Here we show that the distribution of BMI in the Framingham Offspring Study is different from the national distribution. To understand the nature of the difference we can compare observed and expected frequencies or observed and expected proportions (or percentages). The frequencies are large because of the large sample size, the observed percentages of patients in the Framingham sample are as follows: 0.6% underweight, 28% normal weight, 41% overweight and 30% obese. In the Framingham Offspring sample there are higher percentages of overweight and obese persons (41% and 30% in Framingham as compared to 36% and 23% in the national data), and lower proportions of underweight and normal weight persons (0.6% and 28% in Framingham as compared to 2% and 39% in the national data). Are these meaningful differences?

In the module on hypothesis testing for means and proportions, we discussed hypothesis testing applications with a dichotomous outcome variable in a single population. We presented a test using a test statistic Z to test whether an observed (sample) proportion differed significantly from a historical or external comparator. The chi-square goodness-of-fit test can also be used with a dichotomous outcome and the results are mathematically equivalent.  

In the prior module, we considered the following example. Here we show the equivalence to the chi-square goodness-of-fit test.

The NCHS report indicated that in 2002, 75% of children aged 2 to 17 saw a dentist in the past year. An investigator wants to assess whether use of dental services is similar in children living in the city of Boston. A sample of 125 children aged 2 to 17 living in Boston are surveyed and 64 reported seeing a dentist over the past 12 months. Is there a significant difference in use of dental services between children living in Boston and the national data?

We presented the following approach to the test using a Z statistic. 

• Step 1. Set up hypotheses and determine level of significance

H 0 : p = 0.75

H 1 : p ≠ 0.75                               α=0.05

We must first check that the sample size is adequate. Specifically, we need to check min(np 0 , n(1-p 0 )) = min( 125(0.75), 125(1-0.75))=min(94, 31)=31. The sample size is more than adequate so the following formula can be used

This is a two-tailed test, using a Z statistic and a 5% level of significance. Reject H 0 if Z < -1.960 or if Z > 1.960.

We now substitute the sample data into the formula for the test statistic identified in Step 2. The sample proportion is:

We reject H 0 because -6.15 < -1.960. We have statistically significant evidence at a =0.05 to show that there is a statistically significant difference in the use of dental service by children living in Boston as compared to the national data. (p < 0.0001).  

We now conduct the same test using the chi-square goodness-of-fit test. First, we summarize our sample data as follows:

H 0 : p 1 =0.75, p 2 =0.25     or equivalently H 0 : Distribution of responses is 0.75, 0.25 

We must assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ...,np k >) > 5. The sample size here is n=125 and the proportions specified in the null hypothesis are 0.75, 0.25. Thus, min( 125(0.75), 125(0.25))=min(93.75, 31.25)=31.25. The sample size is more than adequate so the formula can be used.

Here we have df=k-1=2-1=1 and a 5% level of significance. The appropriate critical value is 3.84, and the decision rule is as follows: Reject H 0 if χ 2 > 3.84. (Note that 1.96 2 = 3.84, where 1.96 was the critical value used in the Z test for proportions shown above.)

(Note that (-6.15) 2 = 37.8, where -6.15 was the value of the Z statistic in the test for proportions shown above.)

We reject H 0 because 37.8 > 3.84. We have statistically significant evidence at α=0.05 to show that there is a statistically significant difference in the use of dental service by children living in Boston as compared to the national data.  (p < 0.0001). This is the same conclusion we reached when we conducted the test using the Z test above. With a dichotomous outcome, Z 2 = χ 2 !   In statistics, there are often several approaches that can be used to test hypotheses. 

Tests for Two or More Independent Samples, Discrete Outcome

Here we extend that application of the chi-square test to the case with two or more independent comparison groups. Specifically, the outcome of interest is discrete with two or more responses and the responses can be ordered or unordered (i.e., the outcome can be dichotomous, ordinal or categorical). We now consider the situation where there are two or more independent comparison groups and the goal of the analysis is to compare the distribution of responses to the discrete outcome variable among several independent comparison groups.  

The test is called the χ 2 test of independence and the null hypothesis is that there is no difference in the distribution of responses to the outcome across comparison groups. This is often stated as follows: The outcome variable and the grouping variable (e.g., the comparison treatments or comparison groups) are independent (hence the name of the test). Independence here implies homogeneity in the distribution of the outcome among comparison groups.    

The null hypothesis in the χ 2 test of independence is often stated in words as: H 0 : The distribution of the outcome is independent of the groups. The alternative or research hypothesis is that there is a difference in the distribution of responses to the outcome variable among the comparison groups (i.e., that the distribution of responses "depends" on the group). In order to test the hypothesis, we measure the discrete outcome variable in each participant in each comparison group. The data of interest are the observed frequencies (or number of participants in each response category in each group). The formula for the test statistic for the χ 2 test of independence is given below.

Test Statistic for Testing H 0 : Distribution of outcome is independent of groups

and we find the critical value in a table of probabilities for the chi-square distribution with df=(r-1)*(c-1).

Here O = observed frequency, E=expected frequency in each of the response categories in each group, r = the number of rows in the two-way table and c = the number of columns in the two-way table.   r and c correspond to the number of comparison groups and the number of response options in the outcome (see below for more details). The observed frequencies are the sample data and the expected frequencies are computed as described below. The test statistic is appropriate for large samples, defined as expected frequencies of at least 5 in each of the response categories in each group.  

The data for the χ 2 test of independence are organized in a two-way table. The outcome and grouping variable are shown in the rows and columns of the table. The sample table below illustrates the data layout. The table entries (blank below) are the numbers of participants in each group responding to each response category of the outcome variable.

Table - Possible outcomes are are listed in the columns; The groups being compared are listed in rows.

In the table above, the grouping variable is shown in the rows of the table; r denotes the number of independent groups. The outcome variable is shown in the columns of the table; c denotes the number of response options in the outcome variable. Each combination of a row (group) and column (response) is called a cell of the table. The table has r*c cells and is sometimes called an r x c ("r by c") table. For example, if there are 4 groups and 5 categories in the outcome variable, the data are organized in a 4 X 5 table. The row and column totals are shown along the right-hand margin and the bottom of the table, respectively. The total sample size, N, can be computed by summing the row totals or the column totals. Similar to ANOVA, N does not refer to a population size here but rather to the total sample size in the analysis. The sample data can be organized into a table like the above. The numbers of participants within each group who select each response option are shown in the cells of the table and these are the observed frequencies used in the test statistic.

The test statistic for the χ 2 test of independence involves comparing observed (sample data) and expected frequencies in each cell of the table. The expected frequencies are computed assuming that the null hypothesis is true. The null hypothesis states that the two variables (the grouping variable and the outcome) are independent. The definition of independence is as follows:

 Two events, A and B, are independent if P(A|B) = P(A), or equivalently, if P(A and B) = P(A) P(B).

The second statement indicates that if two events, A and B, are independent then the probability of their intersection can be computed by multiplying the probability of each individual event. To conduct the χ 2 test of independence, we need to compute expected frequencies in each cell of the table. Expected frequencies are computed by assuming that the grouping variable and outcome are independent (i.e., under the null hypothesis). Thus, if the null hypothesis is true, using the definition of independence:

P(Group 1 and Response Option 1) = P(Group 1) P(Response Option 1).

 The above states that the probability that an individual is in Group 1 and their outcome is Response Option 1 is computed by multiplying the probability that person is in Group 1 by the probability that a person is in Response Option 1. To conduct the χ 2 test of independence, we need expected frequencies and not expected probabilities . To convert the above probability to a frequency, we multiply by N. Consider the following small example.

The data shown above are measured in a sample of size N=150. The frequencies in the cells of the table are the observed frequencies. If Group and Response are independent, then we can compute the probability that a person in the sample is in Group 1 and Response category 1 using:

P(Group 1 and Response 1) = P(Group 1) P(Response 1),

P(Group 1 and Response 1) = (25/150) (62/150) = 0.069.

Thus if Group and Response are independent we would expect 6.9% of the sample to be in the top left cell of the table (Group 1 and Response 1). The expected frequency is 150(0.069) = 10.4.   We could do the same for Group 2 and Response 1:

P(Group 2 and Response 1) = P(Group 2) P(Response 1),

P(Group 2 and Response 1) = (50/150) (62/150) = 0.138.

The expected frequency in Group 2 and Response 1 is 150(0.138) = 20.7.

Thus, the formula for determining the expected cell frequencies in the χ 2 test of independence is as follows:

Expected Cell Frequency = (Row Total * Column Total)/N.

The above computes the expected frequency in one step rather than computing the expected probability first and then converting to a frequency.  

In a prior example we evaluated data from a survey of university graduates which assessed, among other things, how frequently they exercised. The survey was completed by 470 graduates. In the prior example we used the χ 2 goodness-of-fit test to assess whether there was a shift in the distribution of responses to the exercise question following the implementation of a health promotion campaign on campus. We specifically considered one sample (all students) and compared the observed distribution to the distribution of responses the prior year (a historical control). Suppose we now wish to assess whether there is a relationship between exercise on campus and students' living arrangements. As part of the same survey, graduates were asked where they lived their senior year. The response options were dormitory, on-campus apartment, off-campus apartment, and at home (i.e., commuted to and from the university). The data are shown below.

Based on the data, is there a relationship between exercise and student's living arrangement? Do you think where a person lives affect their exercise status? Here we have four independent comparison groups (living arrangement) and a discrete (ordinal) outcome variable with three response options. We specifically want to test whether living arrangement and exercise are independent. We will run the test using the five-step approach.  

H 0 : Living arrangement and exercise are independent

H 1 : H 0 is false.                α=0.05

The null and research hypotheses are written in words rather than in symbols. The research hypothesis is that the grouping variable (living arrangement) and the outcome variable (exercise) are dependent or related.   

• Step 2.  Select the appropriate test statistic.  

The condition for appropriate use of the above test statistic is that each expected frequency is at least 5. In Step 4 we will compute the expected frequencies and we will ensure that the condition is met.

The decision rule depends on the level of significance and the degrees of freedom, defined as df = (r-1)(c-1), where r and c are the numbers of rows and columns in the two-way data table.   The row variable is the living arrangement and there are 4 arrangements considered, thus r=4. The column variable is exercise and 3 responses are considered, thus c=3. For this test, df=(4-1)(3-1)=3(2)=6. Again, with χ 2 tests there are no upper, lower or two-tailed tests. If the null hypothesis is true, the observed and expected frequencies will be close in value and the χ 2 statistic will be close to zero. If the null hypothesis is false, then the χ 2 statistic will be large. The rejection region for the χ 2 test of independence is always in the upper (right-hand) tail of the distribution. For df=6 and a 5% level of significance, the appropriate critical value is 12.59 and the decision rule is as follows: Reject H 0 if c 2 > 12.59.

We now compute the expected frequencies using the formula,

Expected Frequency = (Row Total * Column Total)/N.

The computations can be organized in a two-way table. The top number in each cell of the table is the observed frequency and the bottom number is the expected frequency.   The expected frequencies are shown in parentheses.

Notice that the expected frequencies are taken to one decimal place and that the sums of the observed frequencies are equal to the sums of the expected frequencies in each row and column of the table.  

Recall in Step 2 a condition for the appropriate use of the test statistic was that each expected frequency is at least 5. This is true for this sample (the smallest expected frequency is 9.6) and therefore it is appropriate to use the test statistic.

We reject H 0 because 60.5 > 12.59. We have statistically significant evidence at a =0.05 to show that H 0 is false or that living arrangement and exercise are not independent (i.e., they are dependent or related), p < 0.005.  

Again, the χ 2 test of independence is used to test whether the distribution of the outcome variable is similar across the comparison groups. Here we rejected H 0 and concluded that the distribution of exercise is not independent of living arrangement, or that there is a relationship between living arrangement and exercise. The test provides an overall assessment of statistical significance. When the null hypothesis is rejected, it is important to review the sample data to understand the nature of the relationship. Consider again the sample data. 

Because there are different numbers of students in each living situation, it makes the comparisons of exercise patterns difficult on the basis of the frequencies alone. The following table displays the percentages of students in each exercise category by living arrangement. The percentages sum to 100% in each row of the table. For comparison purposes, percentages are also shown for the total sample along the bottom row of the table.

From the above, it is clear that higher percentages of students living in dormitories and in on-campus apartments reported regular exercise (31% and 23%) as compared to students living in off-campus apartments and at home (10% each).  

Test Yourself

 Pancreaticoduodenectomy (PD) is a procedure that is associated with considerable morbidity. A study was recently conducted on 553 patients who had a successful PD between January 2000 and December 2010 to determine whether their Surgical Apgar Score (SAS) is related to 30-day perioperative morbidity and mortality. The table below gives the number of patients experiencing no, minor, or major morbidity by SAS category.  

Question: What would be an appropriate statistical test to examine whether there is an association between Surgical Apgar Score and patient outcome? Using 14.13 as the value of the test statistic for these data, carry out the appropriate test at a 5% level of significance. Show all parts of your test.

In the module on hypothesis testing for means and proportions, we discussed hypothesis testing applications with a dichotomous outcome variable and two independent comparison groups. We presented a test using a test statistic Z to test for equality of independent proportions. The chi-square test of independence can also be used with a dichotomous outcome and the results are mathematically equivalent.  

In the prior module, we considered the following example. Here we show the equivalence to the chi-square test of independence.

A randomized trial is designed to evaluate the effectiveness of a newly developed pain reliever designed to reduce pain in patients following joint replacement surgery. The trial compares the new pain reliever to the pain reliever currently in use (called the standard of care). A total of 100 patients undergoing joint replacement surgery agreed to participate in the trial. Patients were randomly assigned to receive either the new pain reliever or the standard pain reliever following surgery and were blind to the treatment assignment. Before receiving the assigned treatment, patients were asked to rate their pain on a scale of 0-10 with higher scores indicative of more pain. Each patient was then given the assigned treatment and after 30 minutes was again asked to rate their pain on the same scale. The primary outcome was a reduction in pain of 3 or more scale points (defined by clinicians as a clinically meaningful reduction). The following data were observed in the trial.

We tested whether there was a significant difference in the proportions of patients reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) using a Z statistic, as follows. 

H 0 : p 1 = p 2    

H 1 : p 1 ≠ p 2                             α=0.05

Here the new or experimental pain reliever is group 1 and the standard pain reliever is group 2.

We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group or that:

In this example, we have

Therefore, the sample size is adequate, so the following formula can be used:

Reject H 0 if Z < -1.960 or if Z > 1.960.

We now substitute the sample data into the formula for the test statistic identified in Step 2. We first compute the overall proportion of successes:

We now substitute to compute the test statistic.

• Step 5.  Conclusion.  

We now conduct the same test using the chi-square test of independence.  

H 0 : Treatment and outcome (meaningful reduction in pain) are independent

H 1 :   H 0 is false.         α=0.05

The formula for the test statistic is:  

For this test, df=(2-1)(2-1)=1. At a 5% level of significance, the appropriate critical value is 3.84 and the decision rule is as follows: Reject H0 if χ 2 > 3.84. (Note that 1.96 2 = 3.84, where 1.96 was the critical value used in the Z test for proportions shown above.)

We now compute the expected frequencies using:

The computations can be organized in a two-way table. The top number in each cell of the table is the observed frequency and the bottom number is the expected frequency. The expected frequencies are shown in parentheses.

A condition for the appropriate use of the test statistic was that each expected frequency is at least 5. This is true for this sample (the smallest expected frequency is 22.0) and therefore it is appropriate to use the test statistic.

(Note that (2.53) 2 = 6.4, where 2.53 was the value of the Z statistic in the test for proportions shown above.)

Chi-Squared Tests in R

The video below by Mike Marin demonstrates how to perform chi-squared tests in the R programming language.

Answer to Problem on Pancreaticoduodenectomy and Surgical Apgar Scores

We have 3 independent comparison groups (Surgical Apgar Score) and a categorical outcome variable (morbidity/mortality). We can run a Chi-Squared test of independence.

H 0 : Apgar scores and patient outcome are independent of one another.

H A : Apgar scores and patient outcome are not independent.

Chi-squared = 14.3

Since 14.3 is greater than 9.49, we reject H 0.

There is an association between Apgar scores and patient outcome. The lowest Apgar score group (0 to 4) experienced the highest percentage of major morbidity or mortality (16 out of 57=28%) compared to the other Apgar score groups.

Teach yourself statistics

Chi-Square Test of Independence

This lesson explains how to conduct a chi-square test for independence . The test is applied when you have two categorical variables from a single population. It is used to determine whether there is a significant association between the two variables.

For example, in an election survey, voters might be classified by gender (male or female) and voting preference (Democrat, Republican, or Independent). We could use a chi-square test for independence to determine whether gender is related to voting preference. The sample problem at the end of the lesson considers this example.

When to Use Chi-Square Test for Independence

The test procedure described in this lesson is appropriate when the following conditions are met:

• The sampling method is simple random sampling .
• The variables under study are each categorical .
• If sample data are displayed in a contingency table , the expected frequency count for each cell of the table is at least 5.

This approach consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.

State the Hypotheses

Suppose that Variable A has r levels, and Variable B has c levels. The null hypothesis states that knowing the level of Variable A does not help you predict the level of Variable B. That is, the variables are independent.

H o : Variable A and Variable B are independent.

H a : Variable A and Variable B are not independent.

The alternative hypothesis is that knowing the level of Variable A can help you predict the level of Variable B.

Note: Support for the alternative hypothesis suggests that the variables are related; but the relationship is not necessarily causal, in the sense that one variable "causes" the other.

Formulate an Analysis Plan

The analysis plan describes how to use sample data to accept or reject the null hypothesis. The plan should specify the following elements.

• Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
• Test method. Use the chi-square test for independence to determine whether there is a significant relationship between two categorical variables.

Analyze Sample Data

Using sample data, find the degrees of freedom, expected frequencies, test statistic, and the P-value associated with the test statistic. The approach described in this section is illustrated in the sample problem at the end of this lesson.

DF = (r - 1) * (c - 1)

E r,c = (n r * n c ) / n

Χ 2 = Σ [ (O r,c - E r,c ) 2 / E r,c ]

• P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a chi-square, use the Chi-Square Distribution Calculator to assess the probability associated with the test statistic. Use the degrees of freedom computed above.

Interpret Results

If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.

Test Your Understanding

A public opinion poll surveyed a simple random sample of 1000 voters. Respondents were classified by gender (male or female) and by voting preference (Republican, Democrat, or Independent). Results are shown in the contingency table below.

Is there a gender gap? Do the men's voting preferences differ significantly from the women's preferences? Use a 0.05 level of significance.

The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:

H o : Gender and voting preferences are independent.

H a : Gender and voting preferences are not independent.

• Formulate an analysis plan . For this analysis, the significance level is 0.05. Using sample data, we will conduct a chi-square test for independence .

DF = (r - 1) * (c - 1) = (2 - 1) * (3 - 1) = 2

E r,c = (n r * n c ) / n E 1,1 = (400 * 450) / 1000 = 180000/1000 = 180 E 1,2 = (400 * 450) / 1000 = 180000/1000 = 180 E 1,3 = (400 * 100) / 1000 = 40000/1000 = 40 E 2,1 = (600 * 450) / 1000 = 270000/1000 = 270 E 2,2 = (600 * 450) / 1000 = 270000/1000 = 270 E 2,3 = (600 * 100) / 1000 = 60000/1000 = 60

Χ 2 = Σ [ (O r,c - E r,c ) 2 / E r,c ] Χ 2 = (200 - 180) 2 /180 + (150 - 180) 2 /180 + (50 - 40) 2 /40     + (250 - 270) 2 /270 + (300 - 270) 2 /270 + (50 - 60) 2 /60 Χ 2 = 400/180 + 900/180 + 100/40 + 400/270 + 900/270 + 100/60 Χ 2 = 2.22 + 5.00 + 2.50 + 1.48 + 3.33 + 1.67 = 16.2

where DF is the degrees of freedom, r is the number of levels of gender, c is the number of levels of the voting preference, n r is the number of observations from level r of gender, n c is the number of observations from level c of voting preference, n is the number of observations in the sample, E r,c is the expected frequency count when gender is level r and voting preference is level c , and O r,c is the observed frequency count when gender is level r voting preference is level c .

The P-value is the probability that a chi-square statistic having 2 degrees of freedom is more extreme than 16.2. We use the Chi-Square Distribution Calculator to find P(Χ 2 > 16.2) = 0.0003.

• Interpret results . Since the P-value (0.0003) is less than the significance level (0.05), we cannot accept the null hypothesis. Thus, we conclude that there is a relationship between gender and voting preference.

Note: If you use this approach on an exam, you may also want to mention why this approach is appropriate. Specifically, the approach is appropriate because the sampling method was simple random sampling, the variables under study were categorical, and the expected frequency count was at least 5 in each cell of the contingency table.

Stats and R

Chi-square test of independence by hand.

• Hypothesis test
• Inferential statistics

Introduction

How the test works, observed frequencies, expected frequencies, test statistic, critical value, conclusion and interpretation.

Chi-square tests of independence test whether two qualitative variables are independent, that is, whether there exists a relationship between two categorical variables. In other words, this test is used to determine whether the values of one of the 2 qualitative variables depend on the values of the other qualitative variable.

If the test shows no association between the two variables (i.e., the variables are independent), it means that knowing the value of one variable gives no information about the value of the other variable. On the contrary, if the test shows a relationship between the variables (i.e., the variables are dependent), it means that knowing the value of one variable provides information about the value of the other variable.

This article focuses on how to perform a Chi-square test of independence by hand and how to interpret the results with a concrete example. To learn how to do this test in R, read the article “ Chi-square test of independence in R ”.

The Chi-square test of independence is a hypothesis test so it has a null ( \(H_0\) ) and an alternative hypothesis ( \(H_1\) ):

• \(H_0\) : the variables are independent, there is no relationship between the two categorical variables. Knowing the value of one variable does not help to predict the value of the other variable
• \(H_1\) : the variables are dependent, there is a relationship between the two categorical variables. Knowing the value of one variable helps to predict the value of the other variable

The Chi-square test of independence works by comparing the observed frequencies (so the frequencies observed in your sample) to the expected frequencies if there was no relationship between the two categorical variables (so the expected frequencies if the null hypothesis was true).

If the difference between the observed frequencies and the expected frequencies is small , we cannot reject the null hypothesis of independence and thus we cannot reject the fact that the two variables are not related . On the other hand, if the difference between the observed frequencies and the expected frequencies is large , we can reject the null hypothesis of independence and thus we can conclude that the two variables are related .

The threshold between a small and large difference is a value that comes from the Chi-square distribution (hence the name of the test). This value, referred as the critical value, depends on the significance level \(\alpha\) (usually set equal to 5%) and on the degrees of freedom. This critical value can be found in the statistical table of the Chi-square distribution. More on this critical value and the degrees of freedom later in the article.

For our example, we want to determine whether there is a statistically significant association between smoking and being a professional athlete. Smoking can only be “yes” or “no” and being a professional athlete can only be “yes” or “no”. The two variables of interest are qualitative variables so we need to use a Chi-square test of independence, and the data have been collected on 28 persons.

Note that we chose binary variables (binary variables = qualitative variables with two levels) for the sake of easiness, but the Chi-square test of independence can also be performed on qualitative variables with more than two levels. For instance, if the variable smoking had three levels: (i) non-smokers, (ii) moderate smokers and (iii) heavy smokers, the steps and the interpretation of the results of the test are similar than with two levels.

Our data are summarized in the contingency table below reporting the number of people in each subgroup, totals by row, by column and the grand total:

Remember that for the Chi-square test of independence we need to determine whether the observed counts are significantly different from the counts that we would expect if there was no association between the two variables. We have the observed counts (see the table above), so we now need to compute the expected counts in the case the variables were independent. These expected frequencies are computed for each subgroup one by one with the following formula:

\[\text{exp. frequencies} = \frac{\text{total # of obs. for the row} \cdot \text{total # of obs. for the column}}{\text{total number of observations}}\]

where obs. correspond to observations. Given our table of observed frequencies above, below is the table of the expected frequencies computed for each subgroup:

Note that the Chi-square test of independence should only be done when the expected frequencies in all groups are equal to or greater than 5. This assumption is met for our example as the minimum number of expected frequencies is 5. If the condition is not met, the Fisher’s exact test is preferred.

Talking about assumptions, the Chi-square test of independence requires that the observations are independent. This is usually not tested formally, but rather verified based on the design of the experiment and on the good control of experimental conditions. If you are not sure, ask yourself if one observation is related to another (if one observation has an impact on another). If not, it is most likely that you have independent observations.

If you have dependent observations (paired samples), the McNemar’s or Cochran’s Q tests should be used instead. The McNemar’s test is used when we want to know if there is a significant change in two paired samples (typically in a study with a measure before and after on the same subject) when the variables have only two categories. The Cochran’s Q tests is an extension of the McNemar’s test when we have more than two related measures.

We have the observed and expected frequencies. We now need to compare these frequencies to determine if they differ significantly. The difference between the observed and expected frequencies, referred as the test statistic (or t-stat) and denoted \(\chi^2\) , is computed as follows:

\[\chi^2 = \sum_{i, j} \frac{\big(O_{ij} - E_{ij}\big)^2}{E_{ij}}\]

where \(O\) represents the observed frequencies and \(E\) the expected frequencies. We use the square of the differences between the observed and expected frequencies to make sure that negative differences are not compensated by positive differences. The formula looks more complex than what it really is, so let’s illustrate it with our example. We first compute the difference in each subgroup one by one according to the formula:

• in the subgroup of athlete and non-smoker: \(\frac{(14 - 9)^2}{9} = 2.78\)
• in the subgroup of non-athlete and non-smoker: \(\frac{(0 - 5)^2}{5} = 5\)
• in the subgroup of athlete and smoker: \(\frac{(4 - 9)^2}{9} = 2.78\)
• in the subgroup of non-athlete and smoker: \(\frac{(10 - 5)^2}{5} = 5\)

and then we sum them all to obtain the test statistic:

\[\chi^2 = 2.78 + 5 + 2.78 + 5 = 15.56\]

The test statistic alone is not enough to conclude for independence or dependence between the two variables. As previously mentioned, this test statistic (which in some sense is the difference between the observed and expected frequencies) must be compared to a critical value to determine whether the difference is large or small. One cannot tell that a test statistic is large or small without putting it in perspective with the critical value.

If the test statistic is above the critical value, it means that the probability of observing such a difference between the observed and expected frequencies is unlikely. On the other hand, if the test statistic is below the critical value, it means that the probability of observing such a difference is likely. If it is likely to observe this difference, we cannot reject the hypothesis that the two variables are independent, otherwise we can conclude that there exists a relationship between the variables.

The critical value can be found in the statistical table of the Chi-square distribution and depends on the significance level, denoted \(\alpha\) , and the degrees of freedom, denoted \(df\) . The significance level is usually set equal to 5%. The degrees of freedom for a Chi-square test of independence is found as follow:

\[df = (\text{number of rows} - 1) \cdot (\text{number of columns} - 1)\]

In our example, the degrees of freedom is thus \(df = (2 - 1) \cdot (2 - 1) = 1\) since there are two rows and two columns in the contingency table (totals do not count as a row or column).

We now have all the necessary information to find the critical value in the Chi-square table ( \(\alpha = 0.05\) and \(df = 1\) ). To find the critical value we need to look at the row \(df = 1\) and the column \(\chi^2_{0.050}\) (since \(\alpha = 0.05\) ) in the picture below. The critical value is \(3.84146\) . 1

Chi-square table - Critical value for alpha = 5% and df = 1

Now that we have the test statistic and the critical value, we can compare them to check whether the null hypothesis of independence of the variables is rejected or not. In our example,

\[\text{test statistic} = 15.56 > \text{critical value} = 3.84146\]

Like for many statistical tests , when the test statistic is larger than the critical value, we can reject the null hypothesis at the specified significance level.

In our case, we can therefore reject the null hypothesis of independence between the two categorical variables at the 5% significance level.

\(\Rightarrow\) This means that there is a significant relationship between the smoking habit and being an athlete or not. Knowing the value of one variable helps to predict the value of the other variable.

Thanks for reading.

I hope the article helped you to perform the Chi-square test of independence by hand and interpret its results. If you would like to learn how to do this test in R, read the article “ Chi-square test of independence in R ”.

As always, if you have a question or a suggestion related to the topic covered in this article, please add it as a comment so other readers can benefit from the discussion.

For readers that prefer to check the \(p\) -value in order to reject or not the null hypothesis, I also created a Shiny app to help you compute the \(p\) -value given a test statistic. ↩︎

Related articles

• Wilcoxon test in R: how to compare 2 groups under the non-normality assumption?
• Correlation coefficient and correlation test in R
• One-proportion and chi-square goodness of fit test
• How to do a t-test or ANOVA for more than one variable at once in R?

Liked this post?

• Get updates every time a new article is published (no spam and unsubscribe anytime):

Yes, receive new posts by email

• Support the blog

FAQ Contribute Sitemap

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.4 chi-square tests, chi-square test of independence section  .

Do you remember how to test the independence of two categorical variables? This test is performed by using a Chi-square test of independence.

Recall that we can summarize two categorical variables within a two-way table, also called an r × c contingency table, where r = number of rows, c = number of columns. Our question of interest is “Are the two variables independent?” This question is set up using the following hypothesis statements:

 \[E=\frac{\text{row total}\times\text{column total}}{\text{sample size}}\]

We will compare the value of the test statistic to the critical value of \(\chi_{\alpha}^2\) with the degree of freedom = ( r - 1) ( c - 1), and reject the null hypothesis if \(\chi^2 \gt \chi_{\alpha}^2\).

Example S.4.1 Section  

Is gender independent of education level? A random sample of 395 people was surveyed and each person was asked to report the highest education level they obtained. The data that resulted from the survey are summarized in the following table:

Question : Are gender and education level dependent at a 5% level of significance? In other words, given the data collected above, is there a relationship between the gender of an individual and the level of education that they have obtained?

Here's the table of expected counts:

So, working this out, \(\chi^2= \dfrac{(60−50.886)^2}{50.886} + \cdots + \dfrac{(57 − 48.132)^2}{48.132} = 8.006\)

The critical value of \(\chi^2\) with 3 degrees of freedom is 7.815. Since 8.006 > 7.815, we reject the null hypothesis and conclude that the education level depends on gender at a 5% level of significance.